Тема 4. Экономический рост
На протяжении всей истории США происходил существенный рост национального дохода. Каждое поколение американцев получало больший доход, чем их родители, и этот более высокий доход позволял им потреблять большее количество товаров и услуг, а более высокий уровень потребления обеспечивал более высокий уровень жизни.
Для того чтобы измерить экономический рост, обычно используют данные о ВНП, суммирующем доходы всех занятых в экономике. Реальный ВНП США в настоящее время более чем в три раза превышает уровень 1950 г., а реальный ВНП на душу населения - более чем в два раза. Прирост действительно заметный и, как показывает приведенная в начале главы цитата, он затрагивает многие грани жизни американского общества.
Существуют значительные различия в уровне жизни в отдельных странах. Таблица 4-1 показывает доход на душу населения (1985 г.) для 12 наиболее населенных стран мира. США возглавляют этот список с доходом 16217 дол./чел. Нигерия имеет душевой доход только 752 дол., что составляет менее 5% от соответствующего показателя для США.
Таблица 4-1.
Межстрановые различия в уровне жизни: 1985 г.
| Страны | Доход на душу населения (дол.) |
| США | 16217 |
| ФРГ | 13857 |
| Япония | 12225 |
| Советский Союз | 8109 |
| Мексика | 5161 |
| Бразилия | 4247 |
| Китай | 3163 |
| Индонезия | 1624 |
| Пакистан | 1492 |
| Индия | 971 |
| Бангладеш | 837 |
| Нигерия | 752 |
1Источник: Summers R., Heston A. A New Set of International Comparisons of Real Product and Price Levels: Estimates for 130 Countries // The Review of Income and Wealth, 1988, March, pp. 1-25. Замечание. Многие аналитики считают, что искаженные отчетные данные по СССР и Китаю делают их статистику крайне ненадежной, и что фактический душевой доход в этих странах намного ниже, чем официально объявленный.
Цель этой главы - объяснить причиныизменения национального дохода во времени, а также межстрановые различия в этом показателе. В главе 3 были рассмотрены факторы производства (капитал и труд), а также производственная технология в качестве источников производства и, следовательно, дохода. Различия в доходе поэтому должны определяться различиями в капитале, труде и технологии.
Наша основнаязадача - представить модель экономического роста, называемую моделью роста Солоу. Проведенный в главе 3 анализ позволил нам описать, как происходит производство, распределение и размещение готовой продукции по направлениям использования в определённый момент времени. Этот анализ был статическим, неким моментальным снимком экономики. Для того чтобы объяснить рост уровня жизни, усовершенствуем технику анализа так, чтобы иметь возможность описать изменения экономики во времени, сделать анализ динамическим (более похожим на фильм, чем на фотографию). Модель роста Солоу показывает, как сбережения, рост населения и технологический прогресс воздействуют на рост объёма производства во времени. Модель также определяет некоторые причины, по которым страны так сильно различаются по уровню жизни населения1.
1Модель роста Солоу названа в честь экономиста Роберта Солоу и была разработана в 1950-1960 гг. В 1987 г. Солоу получил Нобелевскую премию по экономике за работы по теории экономического роста. Модель была впервые опубликована в работе: Solow R. A Contribution to the Theory of Economic Growth // Quarterly Journal of Economics, 1956, February, pp. 65-94
Вторая цель - проанализировать, как экономическая политика может повлиять на уровень жизни и его рост. Модель дает основу, с помощью которой можно проанализировать один из наиболее важных вопросов экономики: какая часть произведенного продукта должна потребляться сегодня, и какая часть его должна сберегаться для использования в будущем. Поскольку сбережения равны инвестициям, сбережения определяют объём капитала, которым экономика будет располагать в будущем. Размеры сбережений находятся под прямым и косвенным влиянием со стороны экономической политики. Оценка разных вариантов политики требует взвешивания всех издержек и выгод выбора того или иного уровня сбережений.
4.1. Накопление капитала
Для того чтобы определить, как связаны между собой рост запасов капитала, рабочей силы и улучшение технологии и как они воздействуют на объем производства, мы используем модель Солоу. Сначала мы проанализируем, как спрос и предложение товаров определяют параметры процесса накопления капитала. Для этого будем считать неизменными объем трудовых ресурсов и используемую технологию. По мере нашего продвижения в обсуждении проблемы экономического роста мы откажемся от этих допущений, чтобы сделать анализ более реалистичным: сначала будет изменяться объем трудовых ресурсов, а затем и технология.
Предложением спрос на произведенную продукцию Спрос и предложение на рынке произведенной продукции, которые были ключевыми элементами статической модели экономики, рассмотренной в главе 3, важны и в модели Солоу. Так же, как и в главе 3 предложение определяет объём производства в каждый момент времени, а спрос определяет распределение продуктов производства между различными направлениями использования.
Предложение и производственная функция. Предложение товаров в модели Солоу описывается с помощью известной нам производственной функции:
Объём производства зависит от запасов капитала и используемого труда. Модель роста Солоу предполагает, что производственная функция обладает свойством постоянной отдачи от масштаба. Напомним, что это свойство выполняется, если
для любого положительного числа z. To есть, если и капитал, и труд умножить на z, то и объём производства увеличится в z раз.
Для простоты соотнесем все величины с количеством работников. Производственная функция с постоянной отдачей от масштаба удобна для этой цели потому, что объём производства на одного рабочего зависит тогда только от количества капитала, приходящегося на одного рабочего. Чтобы убедиться в правильности сказанного, примем z=1/L в приведенном выше определении и получим:
Это уравнение показывает, что объём производства в расчёте на одного работника (Y/L) является функцией капитала на одного работника (K/L).
Мы используем малые буквы для тех количественных показателей, которые относятся к одному рабочему: у=Y/L - выпуск продукции на одного работника или производительность труда, a k=K/L - капитал, приходящийся на одного работникаили капиталовооруженность труда2. Тогда производственную функцию можно записать как
где f(k)=F(k,\;l). Используя производственную функцию, соотносящую производительность труда с капиталовооруженностью, мы значительно упрощаем анализ. На рис. 4-1 изображена эта производственная функция.
2 Мы используем термин "капиталовооруженность" при переводе английского "stock of capital per worker" - это один из случаев, когда термин по-русски звучит более емко и точно, чем его английский прототип. - прим, ред.
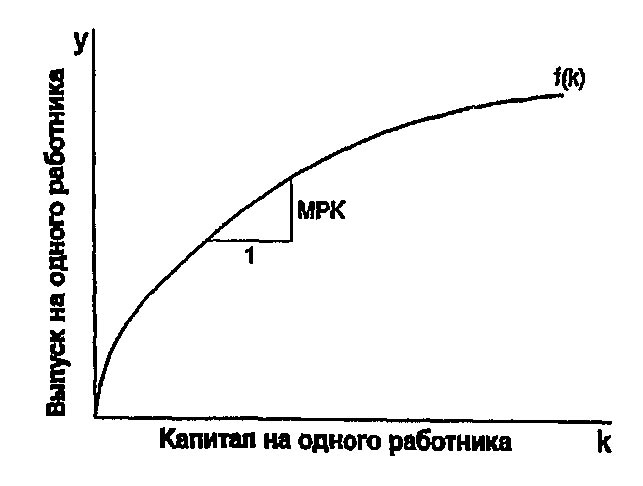
Рис. 4-1. Производственная функция. График производственной функции показывает, как капиталовооруженность k определяет размер выпуска продукции на одного работника y = f(k). Тангенс угла наклона графика производственной функции равен предельной производительности капитала: если k увеличивается на одну единицу, то у возрастает на МРК единиц. По мере возрастания k кривая производственной функции становится более пологой, что свидетельствует о снижении предельной производительности.
Тангенс угла наклона данной производственной функции показывает, сколько дополнительного продукта на одного работника можно получить, если увеличить капиталовооруженность на одну единицу. Эта величина является предельным продуктом капитала МРК. Формально можно приближенно записать:
Заметим, что на рис. 4-1 по мере роста капиталовооруженности график производственной функции становится более пологим, т.е. угол наклона уменьшается. Такая производственная функция характеризуется понижающейся предельной производительностью капитала: каждая дополнительная единица капитала производит меньше продукта, чем предыдущая. Когда запас капитала на одного работника невелик, каждая дополнительная единица капитала дает большую отдачу. Если же капиталовооруженность труда высокая, то дополнительная единица капитала менее эффективна и дает меньше дополнительной продукции.
Спрос на произведенную продукцию и функция потребления. В модели Солоу спрос на товары предъявляется со стороны потребителей и инвесторов. Другими словами, продукция, произведенная каждым рабочим, делится между потреблением, приходящимся на одного рабочего, и инвестициями в расчете на одного рабочего:
Это уравнение сходно с тождеством национальных счетов. Оно немного отличается от уравнения, использованного в главе 3, поскольку опускает государственные закупки (которые пока можно не учитывать) и поскольку оно выражает у, с и i как величины, относящиеся к одному работнику.
Модель Солоу предполагает, что функция потребления принимает простую форму:
где норма сбережения s принимает значения от 0 до 1. Эта функция означает, что потребление пропорционально доходу. Каждый год часть (1-s) дохода потребляется и часть s сберегается.
Роль такой трактовки потребления выяснится, если мы заменим величину с величиной (l-s)y в тождестве национальных счетов:
После преобразования получим:
Это уравнение показывает, что инвестиции (как и потребление) пропорциональны доходу. Если инвестиции равны сбережениям, норма сбережений s также показывает, какая часть произведенной продукции направляется на капитальные вложения.
Устойчивый уровень капиталовооруженности
Представив две главных составляющих модели Солоу - производственную функцию и функцию потребления, можно проанализировать, как накопление капитала обеспечивает экономический рост. Запасы капитала могут изменяться по двум причинам:
- Инвестиции приводят к росту запасов капитала.
- Часть капитала изнашивается, то есть амортизируется, что приводит к уменьшению запасов капитала.
Для того чтобы понять, как изменяются запасы капитала, необходимо найти факторы, определяющие величину инвестиций и амортизации.
Ранее отмечалось, что инвестиции в расчёте на одного работника являются частью продукта, приходящегося на одного работника (sy). Заменив у выражением производственной функции, мы представим инвестиции на одного работника как функцию от капиталовооруженности:
Чем выше уровень капиталовооруженности k, тем выше объем производства f(k) и больше инвестиции i. Это уравнение, которое включает в себя производственную функцию и функцию потребления, связывает существующие запасы капитала k с накоплением нового капитала i. На рис. 4-2 показано, как норма сбережений определяет разделение продукта на потребление и инвестиции для каждого из значений k.
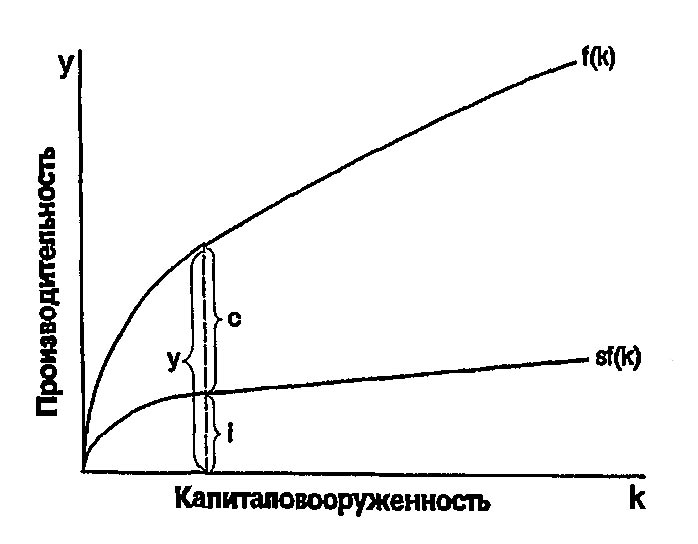
Рис. 4-2. Производство, потребление и инвестиции. Норма сбережений s определяет деление произведённого продукта на потребление и инвестиции. Для любого уровня капиталовооруженности k объём производства есть f(k), инвестиции равны sf(k), а потребление составляет f(fc) - sf(k).
Чтобы учесть в модели амортизацию, предположим, что ежегодно выбывает определенная доля капитала \delta. Назовём \delta нормой выбытия. Например, если капитал эксплуатируется в среднем 25 лет, то норма выбытия равна 4% в год (\delta = 0,04). Таким образом, количество капитала, которое выбывает каждый год, составляет - \delta k. На рис. 4-3 показано, как выбытие зависит от запасов капитала.

Рис. 4-3. Выбытие капитала. Ежегодно выбывает определённая фиксированная часть капитала, поэтому выбытие пропорционально запасам капитала.
Влияние инвестиций и выбытия на запасы капитала можно выразить с помощью следующего уравнения:
т.е.
где \Delta k есть изменение запасов капитала, приходящихся на одного работника за год. Поскольку инвестиции равны сбережениям, изменение запасов капитала может быть записано так:
Это уравнение показывает, что изменение запасов капитала равно инвестициям sf(k) минус выбытие капитала \delta k.
На рис. 4-4 инвестиции и выбытие показаны для различных уровней капиталовооруженности k. Чем выше капиталовооруженность, тем больше объем производства и инвестиции, приходящиеся на одного работника. Однако, чем больше запасы капитала, тем больше и величина выбытия.
На рис. 4-4 показано,что существует единственный уровень капиталовооруженности, при котором инвестиции равны величине износа. Если в экономике достигнут именно такой уровень, то он не будет меняться во времени, поскольку две действующие на него силы (инвестиции и выбытие) точно сбалансированы. Таким образом, приданном уровне капиталовооруженности \Delta k=0. Назовем эту ситуацию состоянием устойчивой капиталовооруженности и обозначим его k\ast.
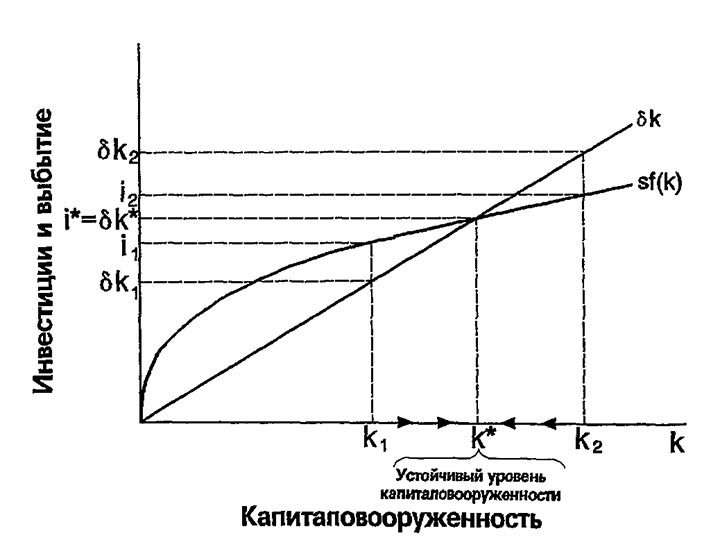
Рис. 4-4. Инвестиции, выбытие и устойчивый уровень капиталовооруженности. Поскольку норма сбережений s постоянна, и сбережения равны инвестициям, объем инвестиций равен sf(k). Поскольку капитал выбывает с постоянной скоростью δ, объем выбытия есть δk. Устойчивый уровень k* - это такая капиталовооруженность работников, при которой инвестиции равны выбытию; в точке k* обе кривые пересекаются. При k<k* инвестиции превышают выбытие, и запасы капитала растут. При k>k* инвестиции меньше выбытия, и запасы капитала уменьшаются.
Приближение к устойчивому состоянию
Устойчивый уровень капиталовооруженности соответствует равновесию экономики в долгосрочном плане. Независимо от первоначального объёма капитала, с которым экономика начинает развиваться, она затем достигает устойчивого состояния.
Предположим, что запасы капитала ниже устойчивого уровня, как это имеет место в точке k_1 на рис. 4-4. В этом случае инвестиции превышают выбытие. Таким образом, капиталовооруженность увеличвается и будет расти вместе с производством до тех пор, пока не приблизится к устойчивому уровню k\ast.
Аналогично предположим, что запасы капитала в начальном состоянии превышают k\ast, например, в точке k_2. В этом случае инвестиции меньше, чем выбытие: капитал выбывает быстрее, чем добавляется. Таким образом, капиталовооруженность будет сокращаться, опять приближаясь к устойчивому уровню. В момент, когда запасы капитала, приходящиеся на одного работника, достигнут устойчивого уровня, инвестиции сравняются с выбытием, и капиталовооруженность не будет ни расти, ни падать.
Движение к устойчивому состоянию: числовой пример
Для того чтобы увидеть, как работает модель Солоу, и как экономика приближается к устойчивому состоянию, рассмотрим числовой пример. Допустим, что производственная функция принимает вид:
т.е. использована производственная функция Кобба-Дугласа с параметром \alpha, равным 1/2.
Получить производственную функцию для одного работника f(k) можно следующим образом. Начнем с определения у:
Заменяя Y производственной функцией, получим:
После преобразования получим:
Поскольку k=K/L, имеем:
Это уравнение может быть также записано как:
т.е. продукт, приходящийся на одного работника, равен корню квадратному из величины запаса капитала, приходящегося на одного рабочего.
Для завершения этого примера предположим, что 30% произведённого продукта идет на сбережения (s=0,3), что 10% запасов капитала выбывает каждый год (\delta=0,1) и что рассматриваемая экономика изначально наделена 4 единицами капитала на одного работника (k=4). Теперь можно проанализировать, что произойдет в экономике через некоторое время.
Начнем с анализа производства и распределения готовой продукции в первом году. В соответствии с производственной функцией, капиталовооруженность, равная 4 единицам, обеспечивает производительность, равную двум единицам продукции на одного работника. Поскольку 70% готовой продукции потребляется и 30% сберегается и инвестируется, то с=1,4, a i=0,6. Кроме того, поскольку 10% запасов капитала выбывает, \delta k=0,4. При инвестициях на уровне 0,6 и амортизации на уровне 0,4 изменение в запасах капитала равно \Delta k=0,2. Поэтому второй год начинается с капиталовооруженностью на уровне 4,2 единицы капитала на одного работника.
Таблица 4-2 показывает, как эта экономика развивается год за годом. Каждый год добавляется новый капитал и растет объём производства. За длительный период экономика достигает устойчивого состояния с 9 единицами капитала на одного работника. В этом устойчивом состоянии инвестиции на уровне 0,9 в точности соответствуют выбытию на уровне 0,9, так что ни запасы капитала, ни производство больше не меняются.
Таблица 4-2.
Приближение к устойчивому состоянию. Количественный пример
| Условия: у=\sqrt k, s=0,3, \delta=0,1 | ||||||
| Годы | k | y | c | i | \delta k | \Delta k |
| 1 2 3 4 5 · 10 · 25 · 100 · · ∞ |
4,000 4,200 4,395 4,584 4,768 5,602 7,321 8,962 9,000 |
2,000 2,049 2,096 2,141 2,184 2,367 2,706 2,994 3,000 |
1,400 1,435 1,467 1,499 1,529 1,657 1,894 2,096 2,100 |
0,600 0,615 0,629 0,642 0,655 0,710 0,812 0,898 0,900 |
0,400 0,420 0,440 0,458 0,477 0,560 0,732 0,896 0,900 |
0,200 0,195 0,189 0,184 0,178 0,150 0,080 0,002 0,000 |
Подобные вычисления за ряд лет - один из возможных путей определения устойчивого уровня капиталовооруженности, однако есть и другой способ, который требует меньшего объема вычислений.
Вспомним, что:
Это уравнение показывает, как изменяется k во времени. Поскольку \Delta k=0 в устойчивом состоянии, то, следовательно,
или
Это уравнение для соотношения капитала и выпуска на одного работника дает возможность определить устойчивый уровень капиталовооруженности k*. После подстановки условий нашего примера получается:
Значение k* может быть найдено возведением в квадрат обеих частей этого уравнения. Таким путем можно определить, что устойчивая капиталовооруженность составляет 9 единиц на рабочего, что подтверждает справедливость расчетов, приведенных в табл. 4-2.
ПРИМЕР 4-1
Послевоенный рост экономики в Германии и Японии
Япония и Германия представляют примеры успешного экономического роста. Сегодня они являются экономическими сверхдержавами, однако в 1945 г., в конце второй мировой войны, экономика обеих стран была в полной разрухе. Большая часть основных фондов в этих странах была уничтожена в ходе войны. Однако в течение нескольких десятилетий после окончания войны эти две страны входили в группу государств с самыми высокими темпами экономического роста в мире. В Японии в период между 1948 и 1972 г. производство на душу населения росло на 8,2%3 в год, а в Германии (Западной) - на 5,7% в год. В тр же время в США темп прироста этого показателя составлял только 2,2%.
Является ли послевоенный опыт Японии и Германии неожиданным с точки зрения модели роста Солоу? Рассмотрим экономику в устойчивом состоянии, а затем предположим, что война разрушила часть имевшихся запасов капитала (на рис 4.4 запасы капитала уменьшаются с k\ast до k_1). He удивительно, что уровень производства незамедлительно снизится. Но поскольку норма сбережений (доля продукта, идущая на сбережения и инвестиции) неизменна, экономика постепенно вернется к прежнему устойчивому состоянию. Для этого требуется период очень быстрого роста. Ускорение роста происходит из-за того, что принизком уровне капиталовооруженности инвестиции превышают выбытие и, таким образом, производство растет, поскольку инвестициями обеспечивается большее количество нового капитала, чем его выбывает. Хотя разрушение части основных фондов немедленно снижает выпуск продукции, за этим следует более быстрый, чем обычно, рост. "Экономическое чудо" быстрого роста Японии и Германии (как это часто называется в прессе) полностью соответствует предсказаниям модели Солоу в отношении стран, в которых война резко сократила запасы капитала.
Объяснение японского и германского экономического роста, однако, не ограничивается столь простыми выкладками. Обе страны имеют более высокий уровень сбережений, чем США, и поэтому движутся к другой точке устойчивого состояния. Для того чтобы полнее понять межстрановые различия, необходимо подробнее рассмотреть влияние различия норм сбережения на экономический рост.
3В качестве темпа роста автор использует показатель, который в отечественной экономической статистике называется темпом прироста. Если некоторая величина увеличивается на 2% в год, то в международной статистике принято говорить, что темп роста составляет 2%, и лишь в статистике некоторых бывших социалистических стран будет считаться, что темп роста составляет 102%, а 2% - это годовой прирост. - Прим. ред.
Изменения нормы сбережений
Рассмотрим, что происходит в экономике, когда возрастает норма сбережений. На рис. 4-5 представлены последствия такого изменения. Предположим, что экономика начинает развиваться, находясь в устойчивом состоянии при норме сбережений s_1 и запасах капитала k_1^\ast. Норма сбережений затем возрастает с s_1 до s_2, вызывая соответствующий сдвиг вверх кривой sf(k). При начальном уровне сбережений s_1 и начальных запасах капитала k_1^\ast, инвестиции как раз компенсируют выбытие капитала. Сразу после повышения нормы сбережений инвестиции увеличиваются, но запас капитала, и, следовательно, выбытие остаются пока неизменными; в итоге инвестиции превышают выбытие. Капитал будет постепенно расти до тех пор, пока экономика не достигнет нового устойчивого состояния k_2^\ast с большей капиталовооруженностью и более высокой производительностью труда, чем в прежнем устойчивом состоянии.
Модель Солоу показывает, что норма сбережений является ключевой детерминантой величины устойчивой капиталовооруженности. Если норма сбережений более высока, то экономика будет иметь при прочих равных больший запас капитала и более высокий уровень производства.
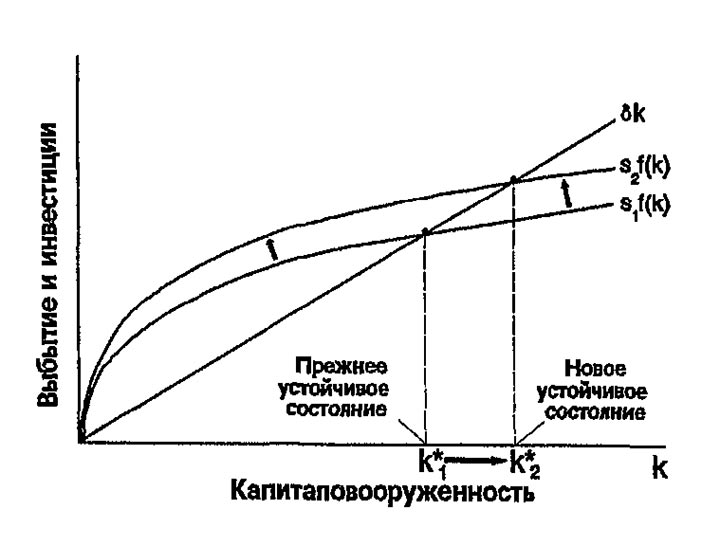
Рис. 4-5. Рост нормы сбережений. Рост нормы сбережений s означает, что размер инвестиций при любых уровнях капиталовооруженности станет больше. Поэтому происходит сдвиг вверх функции сбережений. В точке прежнего устойчивого состояния инвестиции теперь превосходят выбытие. Запасы капитала растут, пока экономика не достигнет нового устойчивого состояния с большей капиталовооруженностью и производительностью.
Какова зависимость между нормой сбережений и экономическим ростом? Более высокие сбережения ведут к более быстрому росту, но это ускорение длится не вечно. Увеличение нормы сбережений обеспечивает рост до тех пор, пока экономика не достигнет нового устойчивого состояния. Если в экономике поддерживается высокая норма сбережений, то и капиталовооруженность, и производительность будут высоки, но сохранить высокие темпы экономического роста навечно не удастся.
ПРИМЕР 4-2
Сбережения в богатых и бедных странах
В соответствии с моделью Солоу страна, которая направляет значительную часть дохода на сбережения, будет иметь высокую устойчивую капиталовооруженность труда и, вследствие этого, высокий уровень душевого дохода. Это не чисто теоретический вывод, так как он подтверждается значительным количеством наблюдений.
На рис. 4-6 показаны данные по 112 странам. На этом рисунке представлено большинство стран мира (исключены нефтедобывающие страны и страны, где в 1960-1985 гг. существовали коммунистические режимы). Приведенные данные показывают положительную связь между долей конечного продукта, идущей на инвестиции, и уровнем душевого дохода. Так, например, страны с высоким уровнем инвестиций (США, Канада или Япония)обычно имеют высокий душевой доход, в то время как страны с низким уровнем инвестиций (Эфиопия, Заир, Чад) имеют низкий доход на душу населения. Международный опыт, таким образом, подтверждает предсказания модели Солоу о том, что норма сбережений является важнейшей детерминантой богатства или бедности страны.
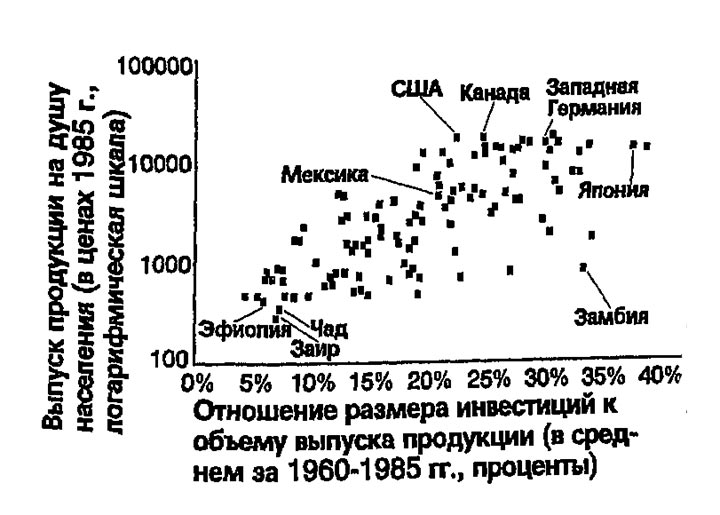
Рис. 4-6. Международные данные о норме инвестиций и душевом доходе.4 На этом рисунке приведены данные по 112 странам, каждая из которых представлена одной точкой Горизонтальная ось показывает норму инвестиций (инвестиции в процентах от объема производства в среднем за 1960-1985 гг.), а вертикальная ось показывает доход на душу населения (производствона одного человека в дол. 1985 г.). Высокий доход на душу населения связан с высокими инвестициями, как и предсказывает модель Солоу.
4Источники: Summers R. and Heston F. A New Set of International Comparison of Real Product and Price Levels: Estimates for 130 Countries // The Review of Income and Wealth, 1988, March, pp. 1-25.
Приведенный рисунок показывает также, что связь между сбережениями и доходом весьма далека от однозначности. Видно, что должны существовать и другие факторы, определяющие величину дохода на душу населения. Мы вновь вернемся к межстрановым различиям позже и затронем некоторые другие аспекты, влияющие на рассматриваемую зависимость.
4.2. Уровень капиталовооруженности и Золотое правило
Теперь, когда проанализирована связь между нормой сбережений и устойчивыми уровнями капитала и дохода, можно обсудить вопрос о том,какие размеры накопления капитала являются оптимальными. В последующем, в разделе 4.5, мы опишем, как государственная экономическая политика влияет на норму сбережений и, таким образом, воздействует на размеры капитала и объем производимой продукции. В настоящем разделе будет изложена теория, лежащая в основе принятия политических решений такого рода. Чтобы сделать анализ простым, предположим, что субъект, принимающий решения, может просто выбрать национальную норму сбережений и соответственно определённое устойчивое состояние. Рассмотрим теперь, какое устойчивое состояние ему следует выбрать.
Сравнение устойчивых состояний
Делая выбор в пользу того или иного устойчивого состояния, политик преследует цель максимизации экономического благосостояния общества. Сами же члены общества не обременены заботой ни об общем количестве капитала в экономике, ни об объёме производства. Для них важно лишь количество товаров и услуг, которое они могут потреблять. Поэтому политик, заинтересованный в экономическом благосостоянии, захочет выбрать устойчивое состояние с наивысшим уровнем потребления. Уровень накопления капитала, обеспечивающий устойчивое состояние с наивысшим уровнем потребления называется Золотым уровнем накопления капитала и обозначается k\ast\ast5.
5Phelps E. The Golden Rule of Accumulation: A Fable for Growthmen // American Economic Review, 1961, vol. 51, September, pp. 638-643.
Как можно узнать, соответствуют ли показатели экономики Золотому правилу? Для того чтобы ответить на этот вопрос, необходимо сначала определить потребление на одного работника в устойчивом состоянии, а затем выяснить, какое из устойчивых состояний обеспечивает наибольшее потребление.
Чтобы найти потребление в устойчивом состоянии, начнем с тождества национальных счетов:
и преобразуем его в
Таким образом, потребление - это производство минус инвестиции. Поскольку целью является определение объёма устойчивого потребления, заменим значения у и i на их величины в условиях устойчивого уровня капиталовооруженности. Выпуск на одного работника, в устойчивом состоянии экономики есть f(k\ast), где k\ast - соответствующая этому состоянию капиталовооруженность. Далее, в устойчивом состоянии капиталовооруженность не изменяется, следовательно, инвестиции равны выбытию, \delta k\ast. Подставляя f(k\ast) вместо у и \delta k\ast вместо i, можно выразить потребление на одного работника в устойчивом состоянии как
Это равенство показывает, что устойчивый уровень потребления есть разница между выпуском и выбытием капитала в устойчивом состоянии. Оно показывает, что увеличивающаяся капиталовооруженность двояко воздействует на величину потребления: она способствует росту выпуска продукции,но в то же время большее количество продукции требуется для возмещения выбытия капитала.
На рис. 4-7 выпуск продукции и выбытие в устойчивом состоянии показаны в виде функции от устойчивой капиталовооруженности. Потребление в устойчивом состоянии - это разница между объёмом производства и выбытием капитала. Рисунок показывает, что существует единственный уровень капиталовооруженности - уровень Золотого правила k\ast\ast, при котором душевое потребление достигает максимума.
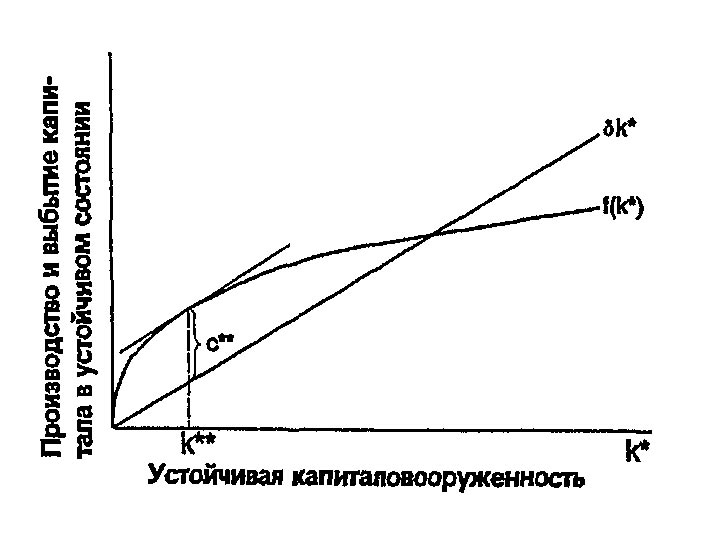
Рис. 4-7. Устойчивый уровень потребления. Произведённая продукция расходуется на потребление или инвестиции. В устойчивом состоянии инвестиции равны выбытию капитала. Поэтому устойчивый уровень потребления есть разница между выпуском f(k*) и выбытием δk*. Устойчивый уровень капиталовооруженности, при котором максимизируется объем потребления, соответствует так называемому Золотому правилу. Капиталовооруженность по Золотому правилу обозначена k**, а потребление по Золотому правилу обозначено с**.
Сравнивая различные устойчивые состояния, необходимо учитывать влияние роста капиталовооруженности как на объём производства, так и на выбытие капитала. С одной стороны, если капиталовооруженность меньше ее уровня по Золотому правилу, то рост запасов капитала вызывает рост производства, превышающий увеличение выбытия. В этом случае потребление растет. Кривая производственной функции наклонена круче, чем линия \delta k\ast, так что расстояние между ними (равное потреблению) растет по мере увеличения k\ast. С другой стороны, если объём капитала превышает уровень Золотого правила, дальнейший рост напиталовооруженности уменьшит потребление, так как рост выпуска продукции окажется меньше прироста выбытия капитала. В этом случае график производственной функциия вляется более пологим, чем линия \delta k\ast, так что расстояние между двумя кривыми (объем потребление) сокращается по мере роста k\ast. При капиталовооруженности, соответствующей уровню Золотого правила, производственная функция и линия \delta k\ast имеют одинаковый наклон, и потребление достигает максимального уровня.
Для того чтобы к этому же выводу прийти другим путем, предположим, что начальная капиталовооруженность равна k\ast, и что рассматривается возможность увеличения капитала до k\ast+1. Объем дополнительного выпуска продукции составит f(k\ast+1)-f(k\ast), что представляет собой предельный продукт капитала МРК.
Прирост выбытия вследствие увеличения капитала на одну единицу есть норма выбытия \delta. Чистый эффект от этой дополнительной единицы капитала (увеличение потребления) составит MPK-\delta, т.е. предельный продукт капитала минус норма выбытия. Если в устойчивом состоянии запас капитала меньше, чем по Золотому правилу, рост капитала увеличивает потребление, поскольку предельный продукт капитала выше, чем норма выбытия.
Если же устойчивый запас капитала превышает уровень Золотого правила, то рост объема капитала снижает потребление, поскольку предельный продукт капитала меньше, чем норма выбытия. Поэтому следующее условие составляет само Золотое правило:
При капиталовооруженности на уровне Золотого правила предельный продукт капитала равен норме выбытия. Другими словами, если Золотое правило выполняется, предельный продукт за вычетом нормы выбытия, MPK-\delta, равен нулю.
Альтернативные уровни устойчивой капиталовооруженности: числовой пример
Рассмотрим механизм выбора устойчивого состояния в нашей гипотетической экономике. Пусть производственная функция будет той же самой, что и в ранее приведенном примере:
Выпуск продукции на одного работника есть корень квадратный из капиталовооруженности труда. На возмещение выбытия капитала уходит 10% от объёма производства. На этот раз выбирается уровень нормы сбережений s и, таким образом, соответствующее устойчивое состояние экономики.
Вспомним, что соотношение "капитал+выпуск" в устойчивом состоянии есть
В нашей экономике это уравнение приобретает следующий вид:
Возведя в квадрат обе части уравнения, найдем величину капиталовооруженности в устойчивом состоянии. Оказывается,
Используя этот результат, можно рассчитать значение капиталовооруженности в устойчивом состоянии для любого уровня нормы сбережений.
В таблице 4-3 представлены результаты расчета показателей, описывающих устойчивые состояния при различных нормах сбережений. Мы видим, что чем выше норма сбережений, тем больше капитал, что в свою очередь ведет к росту выпуска и росту выбытия. Устойчивый уровень потребления (разница между выпуском продукции и выбытием) сначала растет вместе с ростом нормы сбережений, а затем падает. Самый большой уровень потребления достигается, при норме сбережений 0,5; эта норма сбережений обеспечивает устойчивое состояние, соответствующее Золотому правилу.
Другой способ определения устойчивого состояния по Золотому правилу - расчеты на основе предельной производительности капитала. Вспомним из материала главы 3, что для производственной функции Кобба-Дугласа МРК=\alpha y/k. Используя эту формулу и тот факт, что в нашем примере \alpha=1/2, заметим, что две последние колонки таблицы 4.3 показывают величины (МРК-\delta) для различных устойчивых состояний. Напомним ещё раз, что в устойчивом состоянии по Золотому правилу предельный продукт капитала за вычетом выбытия равен нулю.
Таблица 4-3.
Сравнение устойчивых состояний: числовой пример
| Условия: у=\sqrt k, \delta=0,1 | ||||||
| s | k\ast | y\ast | \delta k\ast | c\ast | MPK | МРК-\delta |
| 0,0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1,0 |
0,0 1,0 4,0 9,0 16,0 25,0 36,0 49,0 64,0 81,0 100,0 |
0,0 1,0 2,0 3,0 4,0 5,0 6,0 7,0 8,0 9,0 10,0 |
0,0 0,1 0,4 0,9 1,6 2,5 3,6 4,9 6,4 8,1 10,0 |
0,0 0,9 1,6 2,1 2,4 2,5 2,4 2,1 1,6 0,9 0,0 |
∞ 0,500 0,250 0,167 0,125 0,100 0,083 0,071 0,062 0,056 0,050 |
∞ 0,400 0,150 0,067 0,025 0,000 -0,017 -0,029 -0,038 -0,044 -0,050 |
Переход к устойчивому состоянию, соответствующему Золотому правилу
Пусть теперь решения нашего политика будут более реалистичными. До сих пор мы предполагали, что можно просто выбрать то или иное устойчивое состояние экономики. В этом случае было бы разумно выбрать устойчивое состояние с наиболее высоким уровнем потребления в соответствии с Золотым правилом. Теперь же давайте предположим, что экономика уже достигла устойчивого состояния, не соответствующего Золотому правилу.
Что случится с потреблением, инвестициями и капиталом, если в экономике начнётся переход от одного устойчивого состояния к другому? Могут ли события этого переходного периода заставить субъекта, принимающего решения, отказаться от попытки выйти на траекторию Золотого правила?
Необходимо рассмотреть два случая: когда экономика изначально наделена большимили меньшим объёмом капитала, чем в устойчивом состоянии по Золотому правилу. Второй случай, когда капитала слишком мало, представляется более трудным: необходимо сравнивать преимущества текущего по отношению к будущему потреблению. Как будет показано в разделе 4.5, этот случай актуален для многих стран, включая США.
Экономика начинает развиваться с запасом капитала, большим, чем она могла бы иметь по Золотому правилу. Прежде всего рассмотрим случай, при котором экономика начинает развиваться с запасом капитала большим, чем по Золотому правилу. В этом случае необходимо проводить политику, направленную на снижение нормы сбережений для того, чтобы уменьшить устойчивый уровень запаса капитала. Предположим, что такая политика увенчалась успехом и что в определенный момент времени (назовем его t_0) норма сбережений падает до уровня, который приводит к устойчивому состоянию по Золотому правилу.
Рис. 4.8 показывает, что происходит с производством, потреблением и инвестициями при снижении нормы сбережений. Уменьшение нормы сбережений вызывает немедленное увеличение уровня потребления и снижение уровня инвестиций. Капиталовложения становятся меньшими, чем выбытие капитала. Таким образом, экономика выходит из устойчивого состояния. Постепенно, по мере уменьшения запасов капитала, выпуск продукции, потребление и инвестиции также падают до нового устойчивого состояния. Поскольку в новом состоянии устойчивости устанавливаются пропорции Золотого правила, уровень потребления теперь выше, чем он был до изменения нормы накопления, несмотря даже на то, что производство и инвестиции уменьшились.
Заметим, что по сравнению со старым устойчивым состоянием, потребление выше не только в новой точке устойчивости, но и на всем протяжении пути к этой точке. Когда запас капитала превышает уровень, соответствующий Золотому правилу, снижение нормы сбережений является действительно хорошей политикой, поскольку она ведёт к увеличению потребления в течение всего переходного периода.
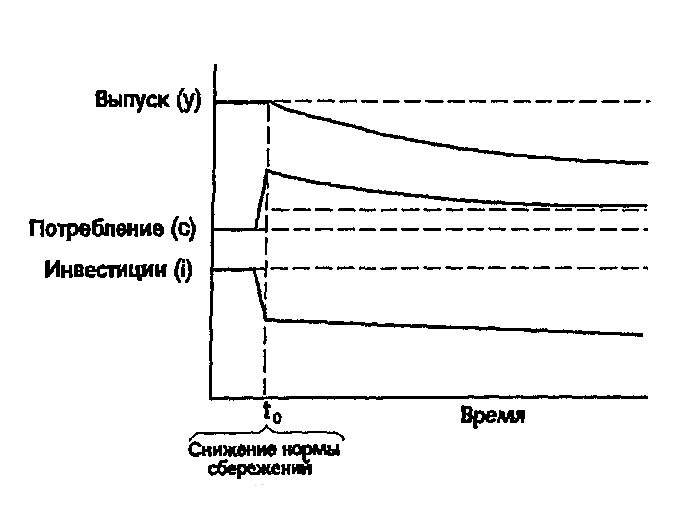
Рис. 4.8. Уменьшение нормы сбережений при начальном капитале, большем, чем по Золотому правилу. Этот рисунок показывает, что происходит во времени с выпуском продукции, потреблением и инвестициями, когда экономика начинает развиваться с капиталом большим, чем по Золотому правилу. Уменьшение нормы сбережений (в момент t0) вызывает немедленный рост потребления и соответствующее снижение инвестиций. По мере уменьшения капиталовооруженности выпуск, потребление и инвестиции одновременно уменьшаются. Но так как исходный запас капитала был слишком высок, потребление в новом устойчивом состоянии выше по сравнению с начальным состоянием.
Экономика начинает развиваться с меньшей капиталовооруженностью, чем при устойчивом состоянии по Золотому правилу. Когда экономика начинает развиваться с меньшей капиталовооруженностью, чем при устойчивом состоянии по Золотому правилу, необходимо увеличить норму сбережений, чтобы достичь точки, соответствующей Золотому правилу. На рис. 4-9 показано, что при этом произойдет. Увеличение нормы сбережений в момент t_0 вызывает немедленное падение потребления и увеличение инвестиций. Рост инвестиций через некоторое время приводит к росту капиталовооруженности. По мере накопления капитала производство, потребление и инвестиции постепенно растут и в конце концов достигают нового устойчивого уровня.
Поскольку потребление в начальном устойчивом состоянии было ниже, чем по Золотому правилу, рост сбережений в конечном счете приводит к более высокому уровню потребления.
Ведет ли рост сбережений, обеспечивающий достижение устойчивого состояния по Золотому правилу, к росту благосостояния? В конечном счете - да, потому что устойчивый уровень потребления будет теперь выше. Но для достижения этого нового устойчивого состояния требуется начальный период с уменьшенным потреблением (в отличие от случая, когда начальная капиталовооруженность выше, чем предусмотрено Золотым правилом).
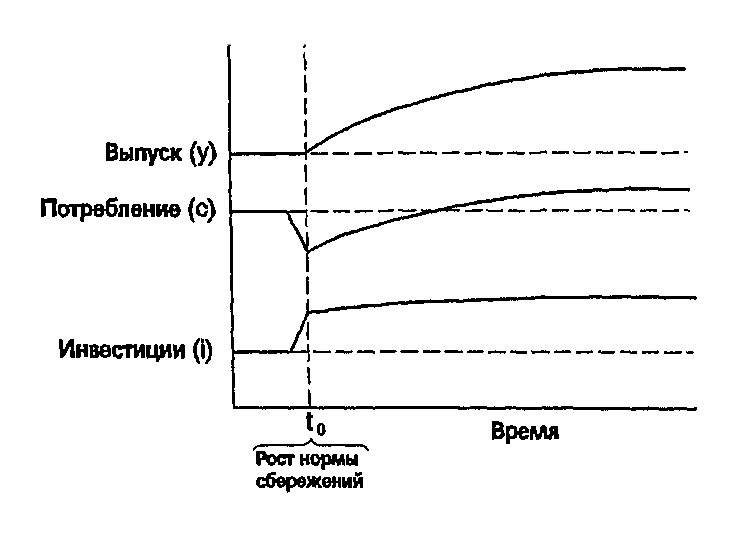
Рис. 4.9. Последствия увеличения нормы сбережений при начальной капиталовооруженности ниже, чем по золотому правилу. На этом рисунке показано, что произойдёт с производством, потреблением и инвестициями, если экономика начинает развиваться с меньшим запасом капитала, чем по Золотому правилу. Увеличение нормы сбережений (в момент t0) вызывает немедленное падение потребления и соответствующий рост инвестиций. По мере роста запасов капитала растут и производство, и потребление, и инвестиции. Поскольку экономика начинала развиваться с меньшим капиталом, чем по Золотому правилу, новое устойчивое состояние имеет более высокий уровень потребления по сравнению с начальным.
Когда начальная капиталовооруженность выше, чем по Золотому правилу, достижение устойчивого состояния с максимумом потребления сопровождается более высоким уровнем потребления в течение всего рассматриваемого периода времени. Когда женачальная капиталовооруженность ниже, чем по Золотому правилу, достижение устойчивого состояния по Золотому правилу требует немедленного снижения потребления в настоящем для того, чтобы повысить его в будущем.
Принятие решения о переходе к устойчивому уровню капиталовооруженности по Золотому правилу затрудняется тем, что состав населения все время обновляется. Достижение уровня Золотого правила приводит в конечном счете к наивысшему устойчивому уровню потребления и потому выгодно будущим поколениям. Но когда начальная капиталовооруженность ниже, чем по Золотому правилу, достижение нового устойчивого уровня требует резкого увеличения инвестиций и соответственно снижения потребления нынешних поколений.
Решение вопроса об увеличении накопления капитала требует сопоставления благосостояния различных поколений. Политик, более озабоченный благосостоянием нынешнего поколения, чем будущих, может решить отказаться от цели достижения устойчивого уровня по Золотому правилу. И наоборот, тот, кто в равной мере заботится обо всех поколениях, будет следовать Золотому правилу. Даже при том, что нынешнее поколение будет потреблять меньше, все будущие поколения воспользуются выгодами того, что выбор был сделан в соответствии с Золотым правилом.
Таким образом, оптимальный темп накопления капитала в решающей степени зависит от того, как соизмеряются интересы нынешнего и будущих поколений. Библейское Золотое правило говорит нам о том, что мы "должны относиться к другим так же, как мы хотели бы, чтобы относились к нам". Если следовать этому принципу, то благополучие любого поколения одинаково важно. Принятие решений в соответствии с Золотым правилом является при такой постановке вопроса оптимальной стратегией, почему, собственно, это правило и называется Золотым.
4.3. Рост населения
Базовая модель Солоу показывает, что само по себе накопление капитала не может объяснить непрерывный экономический рост. Высокий уровень сбережений временно увеличивает темпы роста, но экономика в конце концов приближается к устойчивому состоянию, при котором запасы капитала и объем производства постоянны. Для того чтобы объяснить непрерывный экономический рост, который наблюдается в большинстве стран мира, нужно расширить модель Солоу и включить в нее два других источника экономического роста: рост населения и технологический прогресс. В данном разделе в модель вводится фактор роста населения.
Вместо того, чтобы считать население постоянным (как это было в разделах 4.1 и 4.2), предположим теперь, что население и рабочая сила растут с постоянным темпом n. Например, в США население растет с темпом около 1% в год, т.е. n=0,01. Это означает, что если в этом году работали 150 млн американцев, то в следующем году будет работать 151,5 млн человек (1,01 х 150), на 2-й год будут работать 153,015 млнчеловек (1,01 х 151,5) и т.д.
Устойчивый уровень капиталовооруженности при росте населения
Каким образом рост населения влияет на устойчивое состояние? Для ответа на этот вопрос необходимо обсудить, как рост населения (наряду с инвестициями и выбытием капитала) влияет на капиталовооруженность труда. Как мы отмечали раньше, инвестиции увеличивают запас капитала, а выбытие его уменьшает. Но теперь появилась новая сила, влияющая на количество капитала, приходящегося на одного работника: рост численности работников ведет к сокращению капиталовооруженности каждого из них.
Мы по-прежнему будем использовать малые буквы для обозначения количественных показателей, приходящихся на одного работника. Так, k=K/L - есть капитал на 1 работника и у=Y/L - это выпуск продукции на 1 работника. Не забывайте, однако, что с течением времени количество работников будет расти.
Изменение запаса капитала, приходящегося на одного работника, составит:
Три составляющих в правой части этого уравнения показывают влияние инвестиций, выбытия капитала и роста населения на величину капиталовооруженности. Инвестиции увеличивают k, a выбытие капитала и рост населения уменьшают ее. Мы уже рассматривали это равенство в частном случае, когда n=О.
Для того, чтобы воспользоваться этим равенством, заменим i на sf(k) и перепишемего:
Эффекты выбытия капитала и роста населения теперь объединены. Уравнение показывает, что рост населения уменьшает капиталовооруженность таким же образом, как и выбытие. Выбытие уменьшает k за счет сокращения запасов капитала, в то время как рост населения уменьшает k, распределяя капитал между большим количеством работающих.
Составляющую (\delta+n)k можно рассматривать как критическую величину инвестиций6. Это инвестиции, необходимые для поддержания запаса капитала, приходящегося на одного работника, на постоянном уровне. Критический уровень инвестиций обеспечивает возмещение выбытия капитала, которое равно \delta k. Он также включает инвестиции, необходимые для обеспечения капиталом в прежнем объеме новых работников. Необходимые для этих целей инвестиции составляют nk, поскольку на каждого работника приходится n новых работников и поскольку k есть необходимый уровень капиталовооруженности.
6Англ, "break-even investment". - (Прим. перев.)
Чтобы понять, от чего зависит устойчивый уровень капиталовооруженности, используем рис. 4-10, в котором ситуация, отраженная на рис. 4-4, усложнена за счет включения эффекта роста населения. Экономика находится в устойчивом состоянии, если капитал на одного работника k неизменен. Обозначим устойчивый уровень капиталовооруженности k\ast. Если k меньше, чем k\ast, то фактические инвестиции больше их критической величины, и k растет. Если k больше, чем k\ast, инвестиции меньше, чем критические, и k падает.
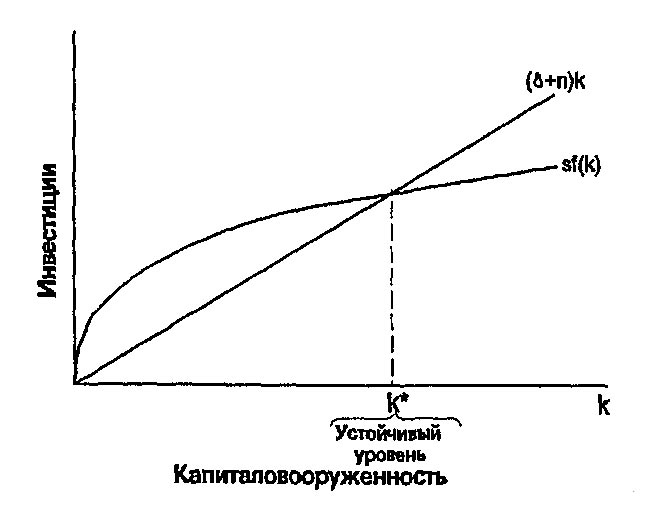
Рис. 4-10. Рост населения в модели Солоу. Подобно выбытию капитала рост населения является одной из причин снижения запаса капитала в расчёте на одного работника. Если n-темп роста населения, а δ-норма выбытия капитала, то (δ+n)k-объем инвестиций, необходимый для поддержания капиталовооруженности на постоянном уровне. Для того чтобы экономика была в устойчивом состоянии, инвестиции sf(k) должны компенсировать последствия выбытия капитала И роста населения - (δ+n)k, что представлено на рисунке точкой пересечения двух кривых.
В устойчивом состоянии положительное влияние инвестиций на величину капиталовооруженности в точности компенсирует негативное влияние выбытия капитала и роста населения. Так, в точке k\ast \Delta k=0 и i\ast=\delta k\ast+nk\ast. Если экономика достигла состояния устойчивости, инвестиции имеют две цели и две составляющие. Одна из них - замена изнашиваемого капитала (составляющая \delta k\ast), а другая - обеспечение новых рабочих капиталом на уровне устойчивого состояния (составляющая nk\ast).
Последствия роста населения
Рост населения дополняет исходную модель Солоу по трём направлениям. Во-первых, он позволяет приблизиться к объяснению причин экономического роста. В устойчивом состоянии экономики при растущем населении капитал и выпуск продукции на одного работника остаются неизменными, но поскольку количество работников растет с темпом n, капитал и объем производства тоже растут с темпом n. Следовательно, рост населения не может объяснить длительного роста уровня жизни, поскольку объем производства в расчёте на одного работника в устойчивом состоянии остаётся постоянным. Однако рост населения может объяснить непрерывный рост валового выпуска продукции.
Во-вторых, рост населения позволяет дать дополнительное объяснение того, почему некоторые страны богаты, а другие - бедны. Рассмотрим последствия ускорения роста населения. На рис. 4-11 показывало, что увеличение темпа прироста населения с n_1 до n_2 уменьшает капиталовооруженность устойчивого состояния с k_1^\ast до k_2^\ast. Поскольку k\ast уменьшается, а у\ast=f(k\ast), постольку производительность у\ast тоже снижается. Так модель Солоу предсказывает, что, страны с более высокими темпами роста населения будут иметь более низкий уровень ВНП на душу населения.
В-третьих, рост населения влияет на уровень накопления капитала по Золотому правилу. Вспомним, что потребление на одного работника равно
Поскольку устойчивый объём производства есть f(k\ast), а инвестиции устойчивого состояния - это (\delta+n)k\ast, устойчивый уровень потребления можно определить как
Уровень k\ast, который максимизирует потребление, таков, что МРК=\delta+n, или соответственно МРК-\delta=n.
В устойчивом состоянии по Золотому правилу предельный продукт капитала минус норма выбытия равен темпу прироста населения.
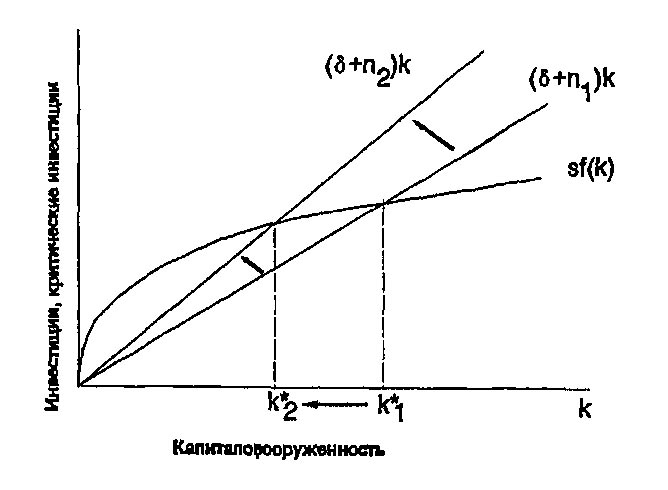
Рис. 4-11. Влияние роста населения. Увеличение темпа роста населения п сдвигает вверх линию, представляющую рост населения и износ. Для нового устойчивого уровня характерен меньший запас капитала на одного рабочего Так, модель Солоу предсказывает, что страны с более высокими темпами роста населения будут иметь меньшую капиталовооруженность и отсюда - более низкие доходы.
ПРИМЕР 4-3
Рост населения в богатых и бедных странах
В соответствии с моделью Солоу страна с более высокими темпами роста населения будет, при прочих равных, иметь более низкую устойчивую капиталовооруженность труда и поэтому более низкий уровень душевого дохода. Другими словами, быстрый рост населения вызывает тенденцию обнищания страны, поскольку очень трудно поддерживать высокий уровень капиталовооруженности, когда само количество работников быстро растет.
Чтобы выяснить, есть ли свидетельства в пользу этого вывода, вернемся к анализу международной статистики.
На рис. 4-12 представлены данные для тех же 112 стран которые были рассмотрены в примере 4-2. В странах с высокой скоростью роста населения обычно наблюдается низкий уровень душевого дохода. Таким образом, имеется совпадающее с выводами модели Солоу свидетельство того, что темп роста населения является одной из детерминант уровня жизни в стране.
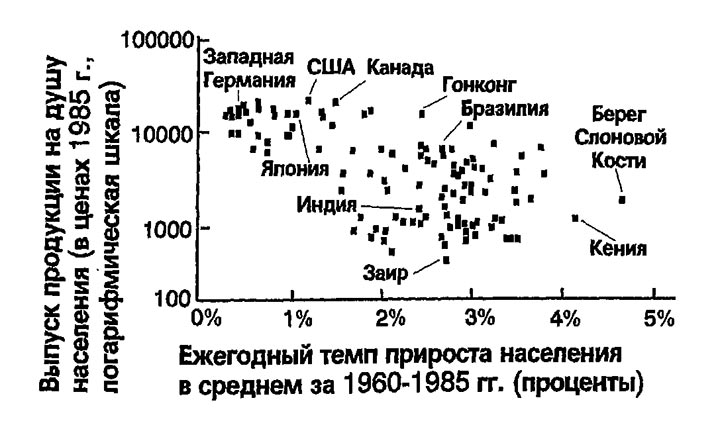
Рис. 4.12. Данные о росте населения и доходе на душу населения в разных странах. На рисунке представленыпоказатели для 112 стран, которые свидетельствуют, что в странах с высокими темпами роста населения обычно наблюдается низкий уровень дохода на душу населения (как и предсказываетмодель Солоу). Источник: см. рис. 4-6.
4.4. Технологический прогресс
Теперь включим в модель Солоу технологический прогресс - третий источник экономического роста. До сих пор предполагалось постоянство соотношения между затратами труда и капитала и выпуском товаров и услуг. Однако модель может быть видоизменена с тем, чтобы она допускала рост общественной производительности под воздействием каких-либо внешних факторов.
Эффективность труда
Для включения в модель технологического прогресса необходимо вернуться к производственной функции, в которой общий объем производства Y соотносится с затратами капитала К и труда L. До сих пор производственная функция записывалась как
Теперь запишем производственную функцию следующим образом:
где Е представляет собой новую переменную, которую мы назовем эффективностью труда одного работника. Эффективность труда зависит от здоровья, образования и квалификации рабочей силы.
Составляющая L\times E представляет собой рабочую силу, измеренную в единицах труда с неизменной эффективностью. Принимается во внимание количество работников L и эффективность труда каждого из них Е. В соответствии с новой производственной функцией общий объем производства Y зависит от количества единиц капитала К и от числа эффективных единиц рабочей силы, т.е. от L\times E.
Простейшим допущением относительно технологического прогресса является то, что он вызывает прирост эффективности труда Е с постоянным темпом g. Например, если g=0,02, то отдача от каждой единицы труда увеличивается на 2% в год: объём производства возрастает так, как если бы рабочая сила за год выросла на 2%, Эта форма технологического прогресса называется трудосберегающей, a g называется темпом трудосберегающего технологического прогресса. Поскольку рабочая сила L растет с темпом n и отдача от каждой единицы труда Е растет с темпом g, общее количество эффективных единиц труда L\times E растет с темпом n+g.
Устойчивый уровень капиталовооруженности при технологическом прогрессе
Описание технологического прогресса через приращение эффективности труда делает его аналогичным росту населения. Здесь мы анализируем экономику в количественных единицах, приходящихся на единицу труда с начальной эффективностью. Пусть k=K/(L\times E) есть капитал на единицу труда с постоянной (начальной) эффективностью, а y=Y/(L\times E) - объём производства на единицу труда с постоянной эффективностью. Используя эти определения, можно записать: у=f(k).
Анализ экономики происходит по той же схеме, что и в случае с ростом населения. Уравнение, показывающее изменение k с течением времени, теперь выглядит следующим образом:
Новый элемент этой формулы g, темп технологического прогресса, появляется постольку, поскольку k есть количество капитала в расчёте на единицу труда с постоянной эффективностью. Если величина g велика, то общее количество единиц труда с постоянной эффективностью растет быстро, а прирост капитала на такую единицу труда сравнительно мал и может стать отрицательным.
Как показано на рис. 4-13, включение в рассмотрение технологического прогресса слабо меняет анализ состояния устойчивости. Имеется один уровень k, обозначенный k\ast, при котором капитал и выпуск, приходящиеся на единицу труда с неизменной эффективностью, постоянны. Это устойчивое состояние представляет собой долгосрочное равновесие экономики.
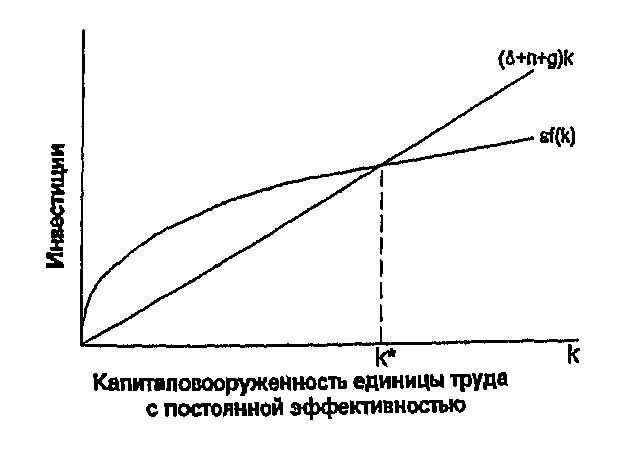
Рис. 4.13. Технологический прогресс. Учёт трудосберегающего технологического прогресса влияет на наш анализ таким же образом, как и учёт фактора роста населения. Теперь, когда k определено как капиталовооруженность единицы труда, имеющей постоянную эффективность, рост отдачи от каждой единицы труда вследствие технологического прогресса вызывает уменьшение k. При устойчивом состоянии экономики инвестиции sf(k) в точности компенсируют уменьшение k вследствие выбытия, роста населения и технологического прогресса.
Последствия технологического прогресса
Таблица 4.4 дает характеристику изменения некоторых переменных модели экономического роста с учетом технологического прогресса. Как мы теперь знаем, капитал на единицу труда с постоянной эффективностью k в устойчивом состоянии неизменен. Поскольку у=f(k), объем выпуска на единицу труда с постоянной эффективностью также неизменен. Вспомним, что количество едиництруда с постоянной эффективностью, приходящихся на одного работника, растет с темпом g. Следовательно, выпуск на одного работника (Y/L=у\times Е) также растет с темпом g. Валовой выпуск \lbrack Y=y\times(E\times L)\rbrack растет с темпом n+g.
Таблица 4-4.
Устойчивый рост в модели Солоу с учетом технологического прогресса
| Переменные | Обозначения | Темп прироста |
| Капитал на единицу труда с постоянной эффективностью | k=K/(EL) | 0 |
| Объем производства на единицу труда с постоянной эффективностью | y=Y/(EL)=f(k) | 0 |
| Объем производства на одного работника | Y/L=yE | g |
| Общий объём производства | Y=y(EL) | n+g |
Таким образом, с учетом технологического прогресса наша модель в конце концов может объяснить, почему уровень жизни растет из года в год. Тем самым мы показали,что технологический прогресс может поддерживать непрерывный рост выпуска продукции на одного работника, тогда как высокий уровень сбережений ведет к высоким темпам роста только до момента достижения устойчивого состояния. Как только экономика достигает устойчивого состояния, темп роста производства на одного работника зависит только от скорости технологического прогресса. Модель Солоу показывает, что только технологический прогресс может объяснить непрерывно растущий уровень жизни.
Введение в модель технологического прогресса изменяет также условия выполнения Золотого правила. Золотое правило для накопления капитала определяет устойчивый уровень, при котором максимизируется потребление на единицу труда с постоянной эффективностью. Следуя тем же самым аргументам, которые использовались ранее, можно показать, что устойчивый уровень потребления на единицу труда с неизменной эффективностью составляет:
Устойчивый уровень потребления максимизируется, если:
или
Таким образом, при запасе капитала по Золотому правилу чистый предельный продукт капитала (МРК-\delta) равен темпу прироста объёма производимой продукции n+g. Поскольку в реальных условиях экономика испытывает воздействие как роста населения, так и технологического прогресса, необходимо использовать это условие для выявления избытка или недостатка капитала по сравнению с устойчивым состоянием по Золотому правилу.
ПРИМЕР 4-4
Устойчивый рост в Соединенных Штатах
После того, как в модель Солоу был введен технологический прогресс и объяснен непрерывный рост уровня жизни, можно задаться вопросом, насколько эта теория соответствует фактам. Модель Солоу предсказывает, что технологический прогресс вызывает одновременный рост многих переменных. В устойчивом состоянии производительность и капиталовооруженность труда растут с тем же темпом, что итехнологический прогресс. Данные по США за последние 40 лет показывают, что производство и капитал на 1 человеко-час фактически росли приблизительно с одним и тем же темпом - около 2% в год.
Технологический прогресс воздействует также на цены факторов производства. В задаче 8(г) в конце этой главы вам предлагается показать, что темп прироста реальной заработной платы при устойчивом состоянии экономики совпадает с темпом технологического прогресса. Реальная цена капитала, однако, постоянна во времени. Опять же эти предсказания оказались справедливыми для США. В течение 40 последних лет реальная заработная плата возрастала на 2% в год, т.е. примерно так же, как и реальный ВНП на человеко-час. В то же время реальная цена капитала (измеряемая как реальный доход на капитал, деленный на запас капитала) оставалась примерно одинаковой.
Предсказания модели Солоу относительно цен факторов производства (и успех этих предсказаний) особенно ценны, если сопоставить их с теорией Карла Маркса о развитии капиталистической экономики. Маркс предсказывал, что эффективность капитала будет со временем падать, и это приведет к экономическому и политическому кризису. Экономическая история не подтвердила предсказаний Маркса, что частично объясняет причину того, почему мы сейчас изучаем теорию роста Солоу, а не теорию роста Маркса.
4.5. Сбережения, рост и экономическая политика
На основе модели Солоу мы раскрыли взаимосвязь различных источников экономического роста. Используя эту теорию, перейдем теперь к анализу экономической политики. Здесь мы рассмотрим три вопроса. Во-первых, должно ли общество сберегать больше или меньше? Во-вторых, как может экономическая политика влиять на норму сбережений? В-третьих, как может экономическая политика влиять на скорость технологического прогресса?
Оценка нормы сбережений
Модель роста Солоу показывает, как норма сбережений определяет устойчивый уровень капиталовооруженности и производительности. Устойчивому состоянию по Золотому правилу соответствует определенное значение нормы сбережений, которое обеспечивает максимум потребления на одного работника и, таким образом, максимизирует экономическое благосостояние. Эти результаты помогают разрешить первый вопрос экономической политики: является ли норма сбережений в экономике слишком низкой, слишком высокой или оптимальной?
Если предельный продукт капитала за вычетом выбытия выше, чем темп прироста объема производства, то экономика функционирует с количеством капитала, меньшим, чем по Золотому правилу. В этом случае рост нормы сбережений в конце концов приведет к устойчивому состоянию при более высоком уровне потребления. С другой стороны, если чистый предельный продукт капитала ниже темпа прироста объема производства, то экономика функционирует со слишком большим количеством капитала, и норма сбережений должна быть уменьшена. Чтобы оценить общенациональный уровень накопления капитала, необходимо сравнить темп прироста объёма производства с величиной чистой отдачи от капитала.
Это сравнение требует оценки темпа прироста (n+g) и оценки чистого предельного продукта капитала (МРК-\delta). Реальный ВНП в США растет со средним темпом 3% в год, поэтому n+g=0,03. Чистый предельный продукт капитала можно рассчитать, основываясь на следующих трех фактах:
- Запас капитала примерно в 2,5 раза больше годового ВНП.
- Выбытие капитала составляет примерно 10% от ВНП.
- На долю капитала приходится около 30% общего годового дохода.
Первое означает, что k=2,5у, а второе, что \delta k=0,1у. Поэтому:
т.е. около 4% запаса капитала выбывает каждый год. Чтобы рассчитать предельный продукт капитала (основываясь на фактах 1 и 3), вспомним наш вывод из третьей главы о том, что доход на капитал равен его предельноу продукту. Поэтому доля капитала - (MPK\times K)\times Y=MPK\times(K\times Y). Подставим теперь значения, вытекающие из фактов 1 и 3:
Это означает, что
Итак, предельный продукт капитала составляет примерно 12% в год. Чистый предельный продукт капитала (МРК-\delta) составляет около 8% в год и намного превосходит средний темп прироста производства, равный 3% в год.
Высокий доход на капитал означает, что запасы капитала в США намного ниже уровня Золотого правила. Этот вывод означает, что при разработке государственной политики следует стремиться к увеличению нормы сбережений и инвестиций. Фактически, в течение многих лет это так и было. Поощрение капиталовложений в течение длительного времени было приоритетным направлением в экономической политике страны.
Изменение нормы сбережений
Государственная политика может привести к увеличению национальной нормы сбережений двумя путями: непосредственно, через увеличение государственных сбережений и косвенно - через создание стимулов для увеличения частных сбережений.
Государственные сбережения представляют собой разницу между государственными доходами и расходами. Если расходы превышают доходы, то правительство сталкивается с бюджетным дефицитом (что означает сбережения со знаком минус). Правительство покрывает дефицит за счет выпуска ценных бумаг, иными словами, занимая деньги. Как мы видели в главе 3, государственный бюджетный дефицит вытесняет инвестиции. Уменьшенный запас капитала - это часть долгового бремени, возлагаемого на будущие поколения. С другой стороны, если доходы превышают расходы, правительство имеет положительное сальдо бюджета. Оно может тогда погасить часть национального долга и начать стимулировать инвестиции.
Частные сбережения могут подвергнуться различного рода воздействиям со стороны правительства. Принятие решений о сбережениях в каждой семье не включено в модель Солоу, но мы можем предположить, что оно зависит от доходности капитала: чем выше доход на капитал, тем более привлекательным становится сбережение. Налоговые стимулы, такие как освобождение от налогов личных пенсионных счетов и льготное налогообложение инвестиций в капитал корпораций, увеличивают доход от капитала и, таким образом, поощряют частные сбережения.
ПРИМЕР 4-5
Социальное страхование и уровень сбережений
Считается, что к государственным программам, воздействующим на частные сбережения, относится система социального страхования. Программа представляет собой систему трансфертных платежей и призвана поддерживать доходы пожилых людей. Трансферты в пользу пенсионеров покрываются за счёт налогообложения фондовзаработной платы работающего населения страны. Эта система снижает потребность копить деньги для существования в старости и, таким образом, может привести к уменьшению объема средств, направляемых на капиталовложения.
Чтобы нейтрализовать отрицательное воздействие социального страхования на национальные сбережения, многие экономисты предлагают реформировать всю эту систему. Современная система такова, что большая часть текущих налоговых поступлений выплачивается нынешнему пожилому поколению. Одно из предложений заключается в том, чтобы все выплаты, которые делаются определённым поколением в трудоспособном возрасте поступали в специальный трастовый фонд; правительство должно затем возвращать эти средства с накопленными процентами этому самому поколению, когда оно достигнет пожилого возраста и уйдет на пенсию. При такой схеме социального страхования рост государственных сбережений будет полностью компенсировать снижение частных сбережений.
Так как воздействие системысоциального страхования на сбережения возможно имеет такое большое значение, многие экономисты пытались оценить величину этого воздействия. Данные, однако, противоречивы. Поэтому среди экономистов нет согласия в вопросе о том, снижает ли система социального страхования объем сбережений в стране и если да, то насколько7.
7Чтобы получить представление об этой дискуссии, см.: Feldstein M.S., Social Security, Induced Retirement and Aggregate Capital Accumulation // Journal of Political Economy 82 (September/October 1974), pp. 905-926; Leimer D.R. and Lesnoy S.D. Social Security and Private Saving: New Time Series Evidence // Journal of Political Economy 90 (June 1982), pp. 606-629; and Feldstein M.S. Social Security and Private Saving: Reply // Journal of Political Economy 90 (June 1982), pp. 630-642.
Поощрение технологического прогресса
Модель Солоу показывает, что постоянный рост дохода на душу населения обусловлен технологическим прогрессом. Модель Солоу, однако, рассматривает технологический прогресс как экзогенный фактор; она не объясняет его. К сожалению, детерминанты технического прогресса недостаточно ясны на сегодняшний день.
Несмотря на это, многие меры государственной политики ориентированы на стимулирование технологического прогресса путём поощрения научных исследований. Например, патентная система дает временную монополию изобретателю нового продукта. Закон о налогах предоставляет льготы научно-исследовательским организациям. Правительственные агентства, такие, как Национальный научный фонд, субсидируют фундаментальные исследования. Подобная государственная политика поощряет использование индивидуальных средств в области технологических разработок.
ПРИМЕР 4-6
Замедление темпов экономического роста в мировом масштабе
Одна из наиболее обескураживающих проблем, с которой столкнулись государственные деятели в течение последних 20 лет - это характерное для всего мира замедление экономического роста, которое началось в начале 1970-х гг. Таблица 4-5 содержит показатели роста реального ВНП на душу населения в семи наиболее развитых странах мира. Темпы роста в США упали с 2,2% до 1,7%. В других странах снижение было такое же или еще более сильное.
Исследования показали, что замедление экономического роста может быть связано с замедлением темпа улучшения производственной функции. В приложении к этой главе показано, как экономисты измеряют улучшение производственной функции, используя переменную, называемую совокупной производительностью факторов. Эта переменная тесно связана с эффективностью труда в модели Солоу. Рост совокупной производительности факторов замедлялся примерно на 1% в год, начиная с 1970 г. Накапливаемые за многие годы даже такие небольшие изменения существенно влияют на экономическоеблагосостояние: вследствие этого 1%-ного снижения роста производительности реальный доход в США примерно на 20% ниже, чем он должен был бы быть.
Таблица 4.5
Замедление роста в различных странах мира
| Рост объёма производства на человека (% в год) | ||
| Страны | 1948-1972 | 1972-1988 |
| Канада | 2,9 | 2,6 |
| Франция | 4,3 | 2,1 |
| Западная Германия | 5,7 | 2,2 |
| Италия | 4,9 | 2,8 |
| Япония | 8,2 | 3,3 |
| Великобритания | 2,4 | 2,1 |
| США | 2,2 | 1,7 |
Источник: Maddison A. Phases of Capitalist Development (Oxford: Oxford University Press.1982);. International Financial Statistics.
Многие экономисты пытались объяснить это неблагоприятное изменение. Ниже приведены некоторые из объяснений.
- Изменение структуры рабочей силы. Пополнение трудовых ресурсов молодым поколением периода бума рождаемости, начавшееся в 70-е гг., снизило средний уровень опытности работников и, следовательно, производительности труда.
- Рост государственного регулирования (например, в сфере охраны окружающей среды) требует от фирм использования менее эффективных методов производства. Регулирование замедляет рост производительности и доходов (даже если с социальной точки зрения оно весьма желательно).
- Рост ценна нефть в 1970-е гг., вызванный политикой стран-членов ОПЕК, сделал часть капитала досрочно устаревшей. Фирмы должны были снять с эксплуатации часть оборудования, которое потребляет много топлива.
- В мире стало меньше новых идей о том, как производить продукцию. Мы вошли в стадию замедления технологического прогресса.
Какое из приведённых объяснений ближе к истине? Все перечисленные объяснения имеют своё рациональное зерно, но какое из них основное - сказать трудно. Замедление экономического роста в мировом масштабе во многом остаётся загадкой8.
8О различных точках зрения на замедление мирового роста см.: Symposium: The Slowdown in Productivity Growth // The Journal of Economic Perspectives 2 (Fall 1988): 3-98. Наряду со статьями различных авторов этот источник содержит обзорную статью Стэнли Фишера.
4.6. Заключение: за пределами модели Солоу
Хотя модель Солоу представляет собой хорошую базу для начала анализа экономического роста, она является лишь первой его ступенью. Модель Солоу сильно упрощает некоторые аспекты реальной жизни иполностью опускает другие. Изучающие экономический рост ученые пытаются построить более сложные модели, которые позволяют им исследовать более широкий круг проблем.
Более совершенные модели обычно превращают одну из экзогенных переменных Солоу в эндогенную переменную. Например, модель Солоу рассматривает норму сбережений как экзогенную переменную. Как нам станет ясно в главе 15, потребление определяется тем, сколько семья решает потреблять сегодня и сколько сберегать на будущее. Более сложные модели роста заменяют функцию потребления модели Солоу теорией поведения домашнего хозяйства9. Далее модель Солоу рассматривает темп роста населения как экзогенную величину. Некоторые более усовершенствованные модели в явном виде включают решения о количестве детей для того, чтобы определить, как выбор размера семьи взаимодействует с другими аспектами экономического роста10. Возможно, наиболее важным является то, что экономисты стараются построить модели для объяснения сложившегося уровня и темпа роста эффективности труда. Некоторые экономисты подчеркивают важность знаний и навыков, получаемых в процессе образования, то есть накопления так называемого человеческого капитала11. Другие полагают, что технологический прогресс есть положительный побочный продукт определенной экономической деятельности; этот побочный продукт называют внешним эффектом. Например, новые улучшенные производственные процессы могут быть разработаны в ходе накопления капитала. Если это соображение правильно, тогда выгода общества от накопления капитала может быть намного больше, чем это предполагается в модели Солоу12.
Модель Солоу показывает, что продолжительный рост уровня жизни может иметь место только в результате технологического прогресса. Поэтому наше понимание экономического роста будет неполным, пока мы не поймем, как решения частных лиц и государственная политика воздействуют на технологический прогресс. Пока это - вопрос, требующий дальнейшего изучения.
9Связь между решением семей о потреблении и моделью накопления капитала существует в нескольких видах. Для оценки различных подходов см. главу 2 и 3 работы Blanchard O.J., Fisher S. Lectures on Macroeconomics.
10Barro R.J., Becker G.S. Fertility Choice in a Model of Economic Growth // Econometrica (March 1989), pp. 481-502.
11Lucas R. Jr. On the Mechanics of Economic Development // Journal of Monetary Economics 22, (1988), pp.3-42; Mankiw G.,Romer D., and Weil D. A Contribution to the Empirics of Economic Growth // Quarterly Journal of Economics, forthcoming.
12Romer P. Crazy Explanations for the Productivity Slowdown // NBER Macroeconomics Annual 2 (1987), pp. 163-201.
Основные выводы.
- Модель Солоу показывает, что норма сбережений в экономике определяет размер запаса капитала,а следовательно, и объем производства. Чем выше норма сбережений, тем больше капиталовооруженность и выше производительность.
- Рост нормы сбережений вызывает период быстрого роста до достижения нового устойчивого состояния. В долгосрочном плане рост нормы сбережений не влияет на темп роста. Продолжительный рост производительности зависит от технологического прогресса.
- Уровень капиталовооруженности, обеспечивающий наибольший объем потребления, называется уровнем Золотого правила. На этом уровне чистый предельный продукт капитала равен темпу прироста производства. Оценки, сделанные для реальных экономик, таких как экономика США, показывают, что запасы капитала намного ниже уровня Золотого правила. Чтобы достичь этого уровня, требуется увеличение инвестиций и, следовательно, снижение уровня потребления нынешних поколений.
- Деятели, ответственные за разработку экономической политики, часто заявляют, что норма накопления капитала должна быть увеличена. Рост государственных сбережений и налоговое стимулирование частных сбережений - таковы способы ускорения накопления капитала.
- Модель Солоу показывает, что темп роста населения также влияет на уровень жизни. Чем выше темп роста населения, тем ниже объём производства в расчёте на одного работника.
- В начале 70-х гг. темп роста производства в большинстве индустриальных государств значительно упал. Причины этого падения не совсем понятны.
Мэнкью Н.Г. Макроэкономика. Пер. с англ. - М.:Изд-во МГУ, 1994.