Тема 31. Теории экономического роста
31.1. Основные темы теории роста
Проблемы экономического роста находились в центре внимания экономистов с давних пор. Среди них можно выделить следующие пять основных групп, значение которых менялось с течением времени:
- факторы экономического роста;
- соотношение настоящих и будущих потребностей и их влияние на темпы роста;
- взаимовлияние экономического роста и распределения дохода;
- историческая тенденция экономического роста;
- условия равновесного (устойчивого, сбалансированного) роста.
31.2. Предыстория
Проблема обеспечения долговременного экономического роста, который играет ключевую роль в процветании или упадке соответствующей державы, занимала центральное место уже в теориях меркантилистов.
Английская классическая школа не имела отдельной специализированной теории экономического роста. Однако она занималась факторами роста национального богатства и его соотношением с распределением дохода. Вопрос о том, чем определяется прирост национального богатства, фактически подразумевается в самом заглавии главного экономического труда Смита: «Исследование о природе и причинах богатства народов». Главный вывод классиков сводился к тому, что прирост богатства определяется величиной факторов производства и их производительностью. (Наиболее подробно этот круг вопросов освещен в I книге «Основ политической экономии» Дж. Ст. Милля, где сначала рассматриваются все факторы производства, затем причины их роста и, наконец, динамика их производительности.) Поскольку предполагалось, что величина естественных факторов производства: труда и земли — в значительной степени не зависит от человеческих усилий, то в качестве основы экономического роста рассматривалось накопление — инвестирование части общественного продукта, которое приводит к возрастанию капитала. Отсюда большое значение, придаваемое «бережливости» английскими классиками, начиная со Смита.
Поскольку основные накопления в то время производились из прибыли капиталистов (наемные рабочие в силу недостаточных доходов, а земельные собственники в силу «потребительской» мотивации сберегали и инвестировали значительно меньше), то особое значение для экономического роста приобретала норма прибыли, а также распределение дохода, благоприятствующее капиталистам.
Что же касается самой нормы прибыли, то классики считали неизбежным ее падение в долгосрочном аспекте. Причиной такого неблагоприятного прогноза был так называемый «закон убывающего плодородия почвы» (см. гл. 4). По мере роста населения и необходимого расширения пахотных площадей убывающее плодородие должно было привести к относительному увеличению ренты и сокращению прибыли, что должно было в итоге привести к падению накопления и прекращению экономического роста. Эта пессимистическая точка зрения, отстаиваемая, в частности, Т. Мальтусом и Д. Рикардо, способствовала тому, что политическая экономия получила имя «мрачной науки» (dismal science).
Представители английской классической школы, очевидно, недооценивали потенциал технического прогресса, который уже во времена Рикардо мог компенсировать убывание естественного плодородия почвы.
Весьма схожих с классической школой взглядов на долговременные перспективы экономического роста при капитализме придерживался и Карл Маркс. Однако тенденцию нормы прибыли к понижению он связывал не с убыванием плодородия почвы, а с ростом отношения постоянного капитала (С), вложенного в средства производства, к переменному капиталу (V), вложенному в рабочую силу, которое он называл «органическим строением капитала»1.
Норма прибыли равна, по Марксу, отношению прибавочной стоимости (m), созданной неоплаченным трудом рабочих, к величине авансированного капитала:
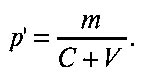
Разделив числитель и знаменатель на V, получим:
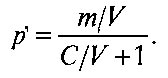
Таким образом, чем больше органическое строение капитала, тем меньше норма прибыли. (Показатель m/V — так называемая «норма эксплуатации» — принимается за неизменную величину при равновесии сил рабочего класса и буржуазии.)
Далее Маркс приходит к выводу, что с развитием капиталистического способа производства происходит относительное уменьшение переменного капитала по сравнению с постоянным капиталом, т.е. возрастание С/V2. Причиной этой тенденции он считает технический прогресс, который, в свою очередь, объясняется желанием капиталистов получить добавочную прибавочную стоимость за счет того, что их издержки производства будут меньше нормальных для данной отрасли3. Очевидно, что Маркс исходит из предпосылки, согласно которой технический прогресс может быть только трудо-, но не капиталосберегающим, т.е. не видит возможности компенсировать увеличение количества применяемых машин на одного работника их удешевлением. Итогом этой тенденции, которая прокладывает себе дорогу через многочисленные противодействующие факторы, является, по Марксу, то, что капиталистическое производство теряет стимул к дальнейшему росту, способ производства сам создает себе пределы4.
С победой маржиналистской революции в экономической теории возобладал статический равновесный подход, и интерес к проблемам роста снизился. Предметом господствующего направления в экономической теории стало распределение уже созданных редких ресурсов между областями их применения. Кроме того, в период с 1871 по 1914 г. экономический рост был для теоретиков скорее презумпцией, чем проблемой. На первый план и в теоретических дискуссиях, и в политических спорах в это время также выходит проблема не роста, а распределения (см. гл. 19).
В наибольшей степени из теоретиков маржинализма проблемами экономического роста занимался А. Маршалл. В подготовительных материалах, которые так и не вошли в «Принципы экономической науки», есть наброски теорий роста, разработанных отдельно для валового и чистого дохода страны. В число факторов роста валового дохода входят:
- число и производительность работников;
- накопленное богатство (капитал);
- естественные ресурсы с учетом удобства их местоположения, уровень техники;
- «общественная безопасность», отражающая уверенность экономических агентов в том, что они получат заработанные доходы.
Рост чистого дохода, т.е. избытка валового дохода общества над его необходимыми тратами, зависит от:
- готовности людей пожертвовать настоящим ради будущего;
- крепости семейных связей (определяющей стимул к обеспечению будущих поколений);
- нормы процента, определяющей стимулы к сбережению.
Естественно, все перечисленные факторы, в свою очередь, зависят от множества других причин. В результате теория становится слишком сложной, многофакторной и необозримой, что, видимо, и послужило причиной того, что Маршалл не включил ее в конечный вариант «Принципов...». В дальнейшем наибольшее развитие получили те теории роста, которые сосредоточивали внимание на узкой группе факторов и взаимосвязей, принимая, прочие за равные.
Значительной попыткой динамизации экономической теории следует считать «Теорию экономического развития» и последующие работы И. Шумпетера, который связывал динамику экономики с предпринимательской деятельностью по осуществлению новых комбинаций (см. гл. 18). Однако в центре внимания Шумпетера был не «количественный» экономический рост, а «качественное» экономическое развитие, и его теория с большим трудом поддавалась формализации и квантификации.
В период между двумя мировыми войнами, который ознаменовался большими потрясениями в экономике развитых западных стран, экономическая теория вновь повернулась лицом к проблемам роста. Огромное значение имела «кейнсианская революция», в ходе которой возникла цельная макроэкономическая теория, оперирующая агрегатными показателями и исследующая условия макроэкономического равновесия, в особенности условия равенства сбережений и инвестиций. В связи с открытиями Кейнса возник большой интерес и к измерению динамики национального дохода и его составляющих (работы С. Кузнеца). Однако сам Кейнс сосредоточил свое внимание на краткосрочном анализе5. Начиная с этого момента, в истории экономической мысли можно выделить сменяющие друг друга периоды преобладания краткосрочной теории цикла (1930-е, 1970-е годы) и долгосрочной теории роста (1940-60-е, 1980-е годы). Легко заметить, что особое внимание к теориям цикла приходилось на периоды ярко выраженных циклических колебаний, тогда как теория роста выходила на первый план в периоды, когда экономическая динамика имела более гладкую траекторию.
31.3. Модель Харрода-Домара
В современной экономической теории под теорией экономического роста имеется в виду формальная теория роста, возникшая как результат распространения кейнсианства на долгосрочный (по Маршаллу) период. Начало этой теории положили модели английского экономиста Роя Харрода и американца Евсея Домара.
Рой Харрод (1900-1978) получил образование в Оксфордском университете (в числе его учителей был Эджуорт), где впоследствии преподавал большую часть своей жизни. Большое влияние оказало на него знакомство с Дж. М. Кейнсом, переросшее в крепкую дружбу. После смерти Кейнса Харрод написал наиболее полную и содержательную его биографию6. В своих ранних микроэкономических произведениях Харрод «воскресил» концепцию предельной выручки Курно7 и представил долгосрочную кривую средних издержек как огибающую краткосрочных кривых8. Но затем область интересов Харрода сдвигается в область макроэкономики и международной экономики. В работе «Теория международной экономики»9 Харрод излагает концепцию мультипликатора внешней торговли. В книге «Экономический цикл»10 он дает экономическому циклу кейнсианское объяснение, усматривая его причину во взаимодействии мультипликатора и акселератора, но без построения соответствующей модели. Дальнейшее исследование этого взаимодействия как раз и привело Харрода к изысканиям в области экономического роста, впервые изложенным в статье 1939 г. «Очерк теории динамики»11, а впоследствии развитым в изданной в 1948 г. книге «К теории экономической динамики».
Харрод всегда стремился к применению экономической теории на практике, во время второй мировой войны работал в администрации премьер-министра У. Черчилля, был экономическим советником правительства, а после войны активно участвовал в разработке нового мирового экономического порядка. За заслуги перед отечеством в 1959 г. ему был присвоен дворянский титул.
Идеи, лежавшие в основе модели экономического роста Харрода, как это часто бывает в истории экономической мысли, высказывались другими авторами раньше опубликования его работ, но получили широкую известность только после выхода в свет книги «К теории экономической динамики».
Шведский экономист Густав Кассель в работе «Теория общественного хозяйства» впервые ввел в экономический анализ понятие сбалансированного роста, при котором структура экономики не меняется, поскольку все ее компоненты растут одинаковым темпом, равным темпу роста населения. (Грубо говоря, сбалансированный рост в динамической экономической теории эквивалентен точке равновесия в статической.) Другой шведский экономист Эрик Лундберг в книге «Исследования по теории экономической экспансии»13 дал понятию сбалансированного роста точную математическую формулировку, показав, что единый темп роста должен равняться отношению между нормой сбережений и показателем капиталоемкости экономики. Этим он практически описал основное содержание будущей модели Харрода-Домара. Однако Харрод не был знаком с работами своих шведских коллег.
Существует несколько вариантов записи модели Харрода, принадлежащих и ему самому, и последующим экономистам. Но во всех случаях модель состоит из трех частей.
1. Фундаментальное уравнение роста. Прежде всего из дефиниций основных экономических агрегатов и тождественных преобразований выводится фундаментальное уравнение Харрода:
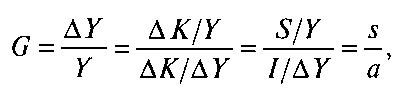
где G — темп прироста дохода или выпуска продукции, Y — доход или выпуск продукции, К — капитал, S — сбережения, I — инвестиции, по определению равные приросту капитала К, по условию равные сбережениям; s — доля сбережений в доходе; а — коэффициент приростной капиталоемкости (количество капитала, необходимое для увеличения выпуска на единицу).
В этой форме фундаментальное уравнение представляет собой достаточно тривиальный вывод: темп роста прямо пропорционален доле сбережений и обратно пропорционален капиталоемкости. Однако ему можно придать и более содержательную интерпретацию с точки зрения исследуемой проблемы стабильности экономического роста.
2.Гарантированный рост. Инвестиции в каждый период времени t зависят от ожидаемого для данного периода прироста выпуска:
It = aΔYt*,
где It — инвестиции в период t, Yt* — ожидаемый доход, a — коэффициент приростной капиталоемкости (количество капитала, необходимое для увеличения выпуска на единицу). Данное равенство фактически представляет собой механизм акселератора.
В то же время сбережения для того же периода по определению равны:
St = sYt*,
где Yt — доход или выпуск продукции в период t, St — сумма сбережений в этот же период, s — доля сбережений в доходе;
По условию St = It, т.е.
sYt = aΔYt*. (2)
Теперь нас интересует ситуация, которая является необходимым условием сбалансированного роста. Это ситуация, когда ожидания предпринимателей выполняются и у них, следовательно, нет никакого стимула расширять или сокращать свои производственные мощности. (Предполагается, что при исполнении желаний мощности загружены полностью.) В этом случае ожидаемый прирост дохода должен быть равен фактическому: ΔYt* = ΔYt, т.е. предприниматели не сталкиваются ни с какими приятными или неприятными сюрпризами.
Тогда из уравнения (2) следует, что:
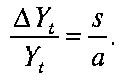
Левая часть уравнения (3) — это тоже темп прироста дохода (или продукта), но не любой, а такой, при котором планы предпринимателей в точности реализуются. Харрод назвал такой рост гарантированным (warranted, или Gw), хотя логичнее, вероятно, было бы назвать его «равновесным».
Величина а в правой части уравнения (3) тоже представляет собой не любой коэффициент приростной капиталоемкости, а только тот, который требуется для гарантированного роста. Ее поэтому можно записать как аr. (индекс r обозначает требуемый (англ. required) уровень данного показателя). «Это новый (предельный. — Прим. авт.) капитал, требуемый для сохранения такого выпуска продукции, который должен удовлетворить потребительский спрос, возникающий из предельного добавочного дохода потребителей» (ΔYt — Прим. авт.)14. В каждый данный момент Харрод рассматривает величину аr как фиксированную. Это означает, что замещение труда капиталом или, наоборот, в процессе производства он считает невозможным. Данную предпосылку, которая, как мы увидим ниже, играет в его модели решающую роль, Харрод выводит не из постоянства технологий, как можно было бы предположить, а из предполагаемой жесткости цен труда и капитала — ставки заработной платы и нормы прибыли. Гибкость первой ограничена закрепленной в обществе минимальной ставкой зарплаты, а гибкость второй — минимально приемлемым уровнем процента.
Таким образом, стабильный гарантированный рост равен:
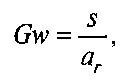
и для каждого момента его величина определена однозначно. Фактический рост вовсе не обязательно должен быть равен гарантированному, хотя, конечно, всякий предприниматель стремится к тому, чтобы его планы были максимально точными15.
Расхождение же этих величин в модели Харрода имеет тенденцию не сглаживаться, а, напротив, нарастать, что ведет к неустойчивости системы. Так, если G > Gw, т.е. рост оказался больше ожидаемого, то капиталоемкость а будет меньше требуемой аr. Это приведет в действие эффект акселератора — возрастут заказы на инвестиционные товары. В свою очередь инвестиционный мультипликатор приведет к дальнейшему росту производства.
Если же фактический рост окажется меньше гарантированного (ожидания производителей окажутся недовыполненными), то мощности окажутся недогруженными, что запустит механизм акселератора-мультипликатора в сторону понижения16.
Возрастающее отклонение фактического роста от гарантированного можно было бы предотвратить, если бы норма сбережения s изменилась во столько же раз, что и фактический темп роста G, но в противоположном направлении. Однако, как справедливо отмечает Харрод, нельзя представить себе, что доля сбережений в доходе должна увеличиться в 4 раза вследствие того, что темп роста дохода изменился с 1 до 4%17.
Таким образом, ситуация сбалансированного роста, когда фактический рост равен гарантированному, оказывается, говоря словами Харрода, «равновесием на лезвии ножа».
Действием этих центробежных сил, заставляющих систему отклоняться все дальше от равновесного роста, Харрод объяснял феномен экономического цикла.
3. Естественный рост. Если гарантированный рост гарантировал полную загрузку производственных мощностей, то далее Харрод вводит в свой анализ предпосылку полной занятости другого фактора производства — трудовых ресурсов. Темп экономического роста при полной занятости труда Харрод назвал естественным — Gn (индекс n соответствует английскому слову natural), хотя, может быть, правильнее было бы назвать его «максимальным». Он определяется темпом роста предложения труда и темпом роста его производительности. При предпосылке экспоненциального роста предложения и производительности труда естественный темп роста равен сумме темпов роста этих величин:
Gn = n + g,
где n — темп роста предложения труда, а g — темп роста производительности труда18. Gn представляет собой максимально возможный уровень среднего значения G за долгосрочный период.
Для того чтобы были полностью загружены и труд и капитал, должно соблюдаться равенство Gw = Gn. Однако гарантированный и естественный темпы роста определяются независимо друг от друга совершенно разными факторами, и совпасть могут только случайно. «Лезвие ножа», на котором находится равновесие в модели Харрода, оказывается «обоюдоострым» — необходимо дополнительно рассмотреть случаи неравенства Gw и Gn.
Для начала, предположим, что Gw < Gn. Выше было сказано, что если G > Gw, возникает самоподдерживающийся бум. Если же при этом к тому же Gw < Gn, т.е. Gw < G < Gn, то этому буму не видно никаких границ в долгосрочном периоде. Структурная безработица присутствует, так как уровень Gn не достигнут, но сокращается. Однако это состояние нельзя назвать беспроблемным, поскольку ситуация, когда производственные мощности хронически перегружены, чревата инфляцией.
Конечно, намного хуже, если Gw > Gn. Тогда G просто не может быть больше Gw (G < Gn < Gw), так как величина Gn — его физический предел. Это означает одновременное существование безработицы (G < Gn) и недогрузки мощностей (Gn < Gw), т.е. преимущественно депрессивное состояние хозяйства в течение долгого времени.
Таким образом, если расхождение фактического и гарантированного роста создает циклические колебания, то расхождение гарантированного и естественного роста ведет к хронической безработице19. Модель Харрода иллюстрирует циклическую и долгосрочную нестабильность капиталистической экономики.
В своих статьях 1946-1947 гг. американский экономист Евсей Домар, не знавший о работе Харрода 1939 г., самостоятельно пришел к уравнению равновесного роста, аналогичного уравнению гарантированного роста Харрода. Основная идея Домара заключалась в том, что инвестиции играют в экономике двойственную роль: с одной стороны, они создают производственные мощности, а с другой — создают спрос через эффект мультипликатора. Домар показал: для того, чтобы прирост спроса соответствовал приросту мощностей, инвестиции (а значит — при условии равновесного роста и весь национальный доход) должны расти темпом, равным os, где о — показатель капиталоотдачи, as — норма сбережений. Поэтому в теории экономического роста принято говорить о модели Харрода-Домара.
31.4. Неоклассическая модель роста Р. Солоу
После второй мировой войны теория роста стала развиваться в ином по сравнению с довоенной депрессией контексте. 1950-е годы стали периодом устойчивого роста. В США бум был связан с Корейской войной, в Западной Европе и в Японии — с американской помощью по плану Маршалла.
Так или иначе, стало ясно, что модель Харрода-Домара сильно преувеличивала неустойчивость западной экономики и недооценивала силы, ведущие к ее росту. С середины 1950-х годов начался новый этап развития теории роста, который продолжался примерно до середины 1970-х, когда на авансцену вышла теория цикла. Ключевую роль на этом этапе сыграла модель роста Р. Солоу.
Американский экономист Роберт Солоу родился в 1924 г. в Нью-Йорке, прошел курс наук и получил докторскую степень в Гарвардском университете. С 1950 г. преподает в Массачусетсском технологическом институте. Основной областью его интересов всегда была макроэкономика, причем его подход заключался в построении моделей, оперирующих несколькими ключевыми показателями и построенных на микроэкономических принципах. Свои научные работы Солоу в основном публиковал в виде журнальных статей и глав в коллективных трудах. Наиболее известными его монографиями являются «Линейное программирование и экономический анализ» (совместно с П. Самуэльсоном и Р. Дорфманом (1958) и «Теория роста: изложение» (1969). За вклад в развитие теории экономического роста в 1987 г. Солоу была присуждена Нобелевская премия. Помимо научных исследований и преподавания Солоу занимался практической деятельностью в государственном секторе. Он входил в штат Совета экономических консультантов при президенте Дж. Кеннеди, позднее работал в государственной комиссии, изучавшей проблемы доходов населения. В конце 1970-х годов Солоу в течение пяти лет был директором Федерального резервного банка Бостона.
Основы модели роста Солоу были изложены в его статье «Вклад в теорию экономического роста»20. Солоу пришел к выводу, что основной причиной неустойчивости экономики в модели Харрода-Домара является фиксированная величина капиталоемкости (а), отражающая жесткое соотношение между факторами производства — трудом и капиталом (K/L). Неудивительно, что в этом случае один из этих факторов часто остается «недогруженным». В соответствии же с принципами неоклассической теории пропорции между капиталом и трудом должны быть переменными (именно в этом заключается неоклассический характер теории роста Солоу)21. Они определяются минимизирующими издержки производителями в зависимости от цен на эти факторы производства. Поэтому вместо фиксированного K/L Солоу включил в свою модель линейно-однородную производственную функцию:
Y = F(K, L).
Разделив все члены на L и обозначив доход на одного работника (Y/L) через у, а капиталоинтенсивность K/L через k, получим:
y = LF(k, l) = Lƒ(k).
Как и в модели Харрода-Домара, предполагается, что население растет неизменным темпом n, а инвестиции составляют постоянную долю дохода, определяемую нормой сбережения s:
I = sY.
Темп прироста k тогда можно записать как:
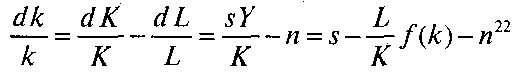
или
dk' = sƒ(k) – nk.
Это так называемое «фундаментальное уравнение» Солоу словами выражается так: прирост капиталовооруженности одного работника — это то, что осталось от удельных инвестиций (сбережений), после того как удалось обеспечить капитальными благами всех дополнительных работников.
Если sƒ(k) = nk, то капиталовооруженность остается прежней (dk = 0), т.е. экономика растет без каких-либо структурных изменений в соотношении между факторами. Это и есть сбалансированный рост.
В модели Солоу в противоположность модели Харрода-Домара траектория сбалансированного роста является устойчивой. Солоу показывает это с помощью следующего графика (рис. 1).
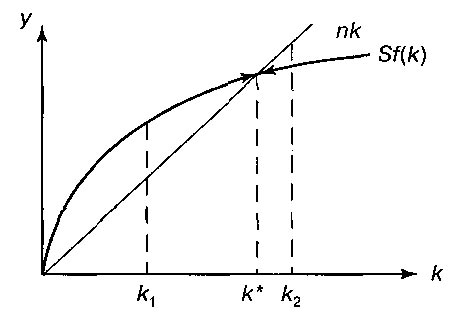
Рис. 1. Графическое отображение модели Солоу
Прямая nk на этом графике показывает, сколько каждый работник должен сберегать и инвестировать из своего дохода, чтобы обеспечить будущих работников (в том числе своих собственных детей) капитальными благами.
Кривая sƒ(k) демонстрирует, каковы его фактические сбережения в зависимости от достигнутого уровня капиталовооруженности. С ростом капиталовооруженности k темп роста инвестиций/сбережений, естественно, падает. Вертикальное расстояние между кривой и прямой обозначает в соответствии с фундаментальным уравнением Солоу дифференциальное изменение показателя капиталовооруженности dk. В точке k* оно равно нулю и наблюдается сбалансированный рост. Во всех точках левее k* (например, k1) капиталовооруженность будет расти, а во всех точках правее k* (например, k2) падать, так что экономика постоянно сдвигается в сторону k* и траектория сбалансированного роста является устойчивой.
В модели Солоу норма сбережений s имеет значение только до выхода экономики на траекторию устойчивого развития: чем больше величина s, тем выше график sk соответственно уровень k*. Но как только рост стал сбалансированным, его дальнейший темп зависит только от роста населения и технологического прогресса.
«Золотое правило». Из модели Солоу следовало, что чем больше норма сбережений, тем выше капиталовооруженность работника в состоянии сбалансированного роста и, следовательно, тем выше темп сбалансированного роста. Но сам по себе рост не является самоцелью. Поэтому следующим шагом, логически вытекающим из модели, было определение условий оптимального для общества экономического роста. Этот шаг одновременно и независимо друг от друга сделали несколько экономистов (Т. Суон, Дж. Мид, М. Алле, Дж. Робинсон, К. фон Вайцзеккер и др.) в самом начале 1960-х годов. Но первым опубликовал ответ на данный вопрос американский экономист Эдмунд Фелпс. Ему же принадлежит и термин «золотое правило накопления капитала», вошедший с тех пор в широкое употребление. Фелпс задался вопросом, какой величины капитал захочет иметь общество, находящееся на траектории сбалансированного роста. Если он будет достаточно большим, это гарантирует высокий уровень производства, но все большая его часть пойдет не на потребление, а на накопление — общество не сможет насладиться плодами роста. Если же объем капитала будет слишком малым, то потреблять можно будет почти все, что произведено, но произведено то будет совсем немного! Где-то посредине между этими двумя крайностями, очевидно, находится оптимальная для общества точка, в которой объем потребления общества является максимальным. Это можно следующим образом показать на графике (рис. 2).
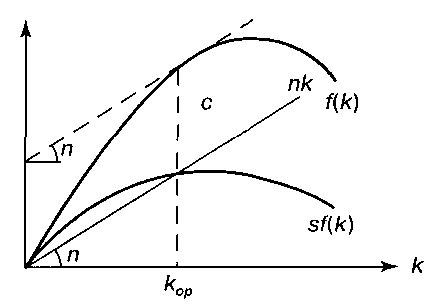
Рис. 2. Графическое отображение максимального объема потребления общества
К графику на рис. 1 мы добавим кривую выпуска или дохода на душу населения у = ƒ(k). Тогда максимизироваться будет вертикальное расстояние между кривой дохода на душу населения и инвестиций на душу населения: ƒ(k) — sƒ(k) = ƒ(k) — nk (в случае сбалансированного роста). Это расстояние является максимальным в точке, где угол наклона касательной к кривой ƒ(k) равен углу наклона прямой nk, т.е. n. Это задает оптимальный уровень капиталоинтенсивности kop. Остается выбрать такую норму потребления/накопления, чтобы кривая sƒ(k) пересекала луч nk в точке, соответствующей kop.
Если мы далее (вместе с перечисленными выше авторами, но за исключением Фелпса) предположим, что в нашей экономике существует совершенная конкуренция на рынках факторов производства и, следовательно, действует теория предельной производительности (см. гл. 17), то угол наклона ƒ(k), т.е. предельная производительность капитала, должен быть равен ставке процента г. В этом случае «золотое правило» можно сформулировать так: ставка процента должна быть равна темпу роста населения, а значит (при сбалансированном росте), и всей экономики:
r = n.
Следовательно, в экономике, испытывающей бурный рост, ставки процента должны при прочих равных условиях быть высокими.
Применимость «золотого правила» на практике оказалась весьма ограниченной ввиду достаточно сильных исходных предпосылок, но оно позволило сформулировать выводы, относящиеся к реальному экономическому росту.
Модель Солоу и «золотое правило» оказались достаточно простыми и чрезвычайно удобными в употреблении аналитическими орудиями. С их помощью оказалось возможно исследовать влияние на экономический рост различных модификаций производственной функции, технического прогресса, изменения нормы сбережений и налогообложения и т.д. Усилиями самого Солоу, Д. Мида и других экономистов модель Солоу была дезагрегирована: отдельно учитывалось производство потребительских и инвестиционных благ. Были созданы также модели, учитывающие «возраст» капитальных благ, поскольку разные их поколения обладают разной производительностью (vintage models). Работы Джеймса Тобина ввели в теорию роста денежную массу (точнее, государственные обязательства, которыми люди владеют наряду с капиталом).
31.6. Новые теории роста
Как уже отмечалось, в 1970-е годы интерес к теории экономического роста упал. Прежде всего это, видимо, было вызвано резкими циклическими колебаниями в западной экономике этого периода. Однако немалую роль сыграло и то обстоятельство, что после изобретения модели Солоу и «золотого правила» дальнейший прогресс в данной области пошел по пути усложнения математической техники без каких-либо прорывов в экономическом содержании.
Однако в 1980-е годы положение вновь изменилось. До тех пор экономистам не удавалось ввести в модель главный фактор экономического роста — технический прогресс, который продолжал оставаться экзогенным. Новые (также чрезвычайно математизированные) теории роста, появившиеся в 1980-е годы, предусматривают положительный внешний эффект (экстерналию) экономического роста, который обеспечивает для экономики источник возрастающей отдачи. Возрастающую общественную отдачу дают, согласно Полу Ромеру, расходы на НИОКР, а согласно Р. Лукасу — инвестиции в человеческий капитал, хотя в каждом индивидуальном случае это вовсе не обязательно. Один из выводов моделей Ромера и Лукаса состоит в том, что экономика, располагающая большими ресурсами человеческого капитала и развитой наукой, имеет в долгосрочной перспективе лучшие шансы роста, чем экономика, лишенная этих преимуществ.
1 Маркс К., Энгельс Ф. Соч. 2-е изд. Т. 26.
2 См.: Маркс К., Энгельс Ф. Соч. 2-е изд. Т. 26. Ч. III. Гл. 13.
3 Там же. Т. 23. Гл. 10.
4 Там же. Т. 26. Ч. III. Гл. 13.
5 Как пишет известный историк экономической мысли И. Ниханс: «Под влиянием «Общей теории» Кейнса внимание экономистов теоретиков переключилось с динамического анализа роста на статический анализ безработицы» (Niehans J. A. History of Economic Theory: Classic Contributions, 1720-1980. Baltimore, London, 1990. P. 452).
6 Harrod R. The Life of John Meynard Keynes. L.: Macmillan, 1951.
7 Harrod R. Economic Essays. L.: Macmillan, 1952. Ch. 3.
8 Ibid. Ch. 4.
9 Harrod R. International Economics. L.: Nisbet, 1933.
10 Harrod R. The Trade Cycle: An Essay. Oxford: Clarendon.
11 Essay in Dynamic Theory // Economic Journal. 1939. Vol. 49. P. 14-33.
12Cassel G. Theoretische Nationalokonomie. 2 Auflage.
13 Lundberg E. Studies in the Theory of Economic Expansion. L., 1937.
14См.: Классики кейнсианства: В 2-х т. Р. Харрод. Э. Хансен. Т. 1. С. 117.
15 Сам Харрод пишет об этом так: «Gw есть величина, определяемая время от времени опытным путем и посредством проб и ошибок, совершаемых великим множеством людей. Было бы большой удачей, если бы в результате их коллективных оценок им удавалось точно достигать величины Gw» (Классики кейнсианства... Т. 1. С. 119).
16 Следует оговориться, что модель Харрода учитывает только эндогенные инвестиции, порождаемые акселерационным механизмом, и абстрагируется от автономных инвестиций, вызванных к жизни новыми изобретениями, долгосрочными ожиданиями и пр.
17 Классики кейнсианства. С. 120.
18 В период времени tYt = LtPt, где L — предложение труда, а Р — производительность труда. Если величина L растет неизменным темпом п процентов, а Р — неизменным темпом n процентов, то Lt = L0ent, a Pt = P0egt. Подставив два последних выражения в первое уравнение, прологарифмировав и продифференцировав по t, получим приведенный в тексте результат.
19 См.: Классики кеинсианства. С. 124.
20 low R. A Contribution to the Theory of Economic Growth // Quarterly Journal of Economics. 1956. February.
21 Хотя, например, в модели общего равновесия Вальраса, ставшей одним из истоков неоклассической теории, предполагалась неизменная пропорция между трудом и капиталом. Да и сам Солоу в своих взглядах на макроэкономические проблемы был скорее кейнсианцем, а не неоклассиком.
22 dk, dK и dL обозначают дифференциальные приросты соответствующих переменных. См. сноску 18 к этой главе.
Автономов В.С. История экономических учений: Учебное пособие. — М.: ИНФРА-М, 2002.