3.1. Понятие факторного анализа

Все явления и процессы хозяйственной деятельности предприятий находятся во взаимосвязи и взаимообусловленности. Одни из них непосредственно связаны между собой, другие косвенно. Отсюда важным методологическим вопросом в экономическом анализе является изучение и измерение влияния факторов на величину исследуемых экономических показателей.

Под экономическим факторным анализом понимается постепенный переход от исходной факторной системы к конечной факторной системе, раскрытие полного набора прямых, количественно измеримых факторов, оказывающих влияние на изменение результативного показателя.

Факторный анализ — методика комплексного и системного изучения и измерения воздействия факторов на величину результативного показателя.

Существуют следующие типы факторного анализа:

1. Детерминированный (функциональный) — результативный показатель представлен в виде произведения, частного или алгебраической суммы факторов.
2. Стохастический (корреляционный) — связь между результативным и факторными показателями является неполной или вероятностной.
3. Прямой (дедуктивный) — от общего к частному.
4. Обратный (индуктивный) — от частного к общему.
5. Одноступенчатый и многоступенчатый.
6. Статический и динамический.
7. Ретроспективный и перспективный.

3.2. Этапы факторного анализа

• 1 этап. Отбор факторов.
• 2 этап. Классификация и систематизация факторов.
• 3 этап. Моделирование взаимосвязей между результативным и факторными показателями.
• 4 этап. Расчет влияния факторов и оценка роли каждого из них в изменении величины результативного показателя.
• 5 этап. Практическое использование факторной модели (подсчет резервов прироста результативного показателя).

3.3. Классификация и систематизация факторов

Классификация факторов по признакам:

• по своей природе:
  
  • основные;
  • второстепенные;
• по степени воздействия на результаты:
  
  • основные
  • второстепенные;
• по отношению к объекту исследования:
  
  • внутренние;
  • внешние;
• по зависимости от коллектива:
  
  • объективные;
  • субъективные;
• по степени распространенности:
  
  • общие;
  • специфические; по времени действия:
  • постоянные;
  • переменные; по характеру действия:
  • экстенсивные;
  • интенсивные;
• по свойствам отражаемых явлений:
  
  • количественные;
  • качественные; по своему составу:
  • сложные;
  • простые;
• по уровню соподчиненности:
  
  • первого порядка;
  • второго порядка;
  • и т.д.
• по возможности измерения влияния:
  
  • измеримые;
  • неизмеримые.

Системный подход в АХД вызывает необходимость взаимосвязанного изучения факторов с учетом их внутренних и внешних связей, взаимодействия и взаимоподчиненности, что достигается с помощью их систематизации (создание факторной системы).

3.4. Виды моделей. Моделирование

По характеру взаимосвязи между показателями различают методы детерминированного и стохастического факторного анализа.

Детерминированный факторный анализ представляет собой методику исследования влияния факторов, связь которых с результативным показателем носит функциональный характер.

Основные свойства детерминированного подхода к анализу:

1. построение детерминированной модели путем логического анализа;
2. наличие полной (жесткой) связи между показателями;
3. невозможность разделения результатов влияния одновременно действующих факторов, которые не поддаются объединению в одной модели;
4. изучение взаимосвязей в краткосрочном периоде.

Моделирование — процесс представления исследуемого показателя с факторами, которое передается в форме конкретного математического уравнения.

Различают четыре типа детерминированных моделей.

1. Аддитивные модели представляют собой алгебраическую сумму показателей и имеют вид:

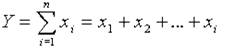
К таким моделям, например, относятся показатели себестоимости во взаимосвязи с элементами затрат на производство и со статьями затрат; показатель объема производства продукции в его взаимосвязи с объемом выпуска отдельных изделий или объема выпуска в отдельных подразделениях.

2. Мультипликативные   модели   в   обобщенном   виде   могут быть представлены формулой:

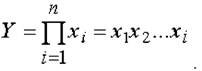
Примером мультипликативной модели является двухфакторная модель объема производства продукции:

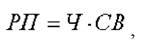
где Ч — среднесписочная численность работников;
CB — средняя выработка на одного работника.

3. Кратные модели:

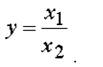
Примером кратной модели служит показатель срока оборачиваемости товаров (в днях) Т_ОБ.Т:

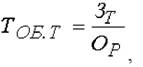
где З_Т — средний запас товаров;
О_Р — однодневный объем реализации.

4. Смешанные модели представляют собой комбинацию перечисленных выше моделей и могут быть описаны с помощью специальных выражений:

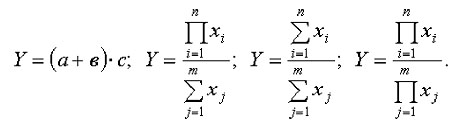
Примерами таких моделей служат показатели затрат на 1 руб. товарной продукции, показатели рентабельности и др.

Для изучения зависимости между показателями и количественного измерения множества факторов, повлиявших на результативный показатель, приведем общие правила преобразования моделей (моделирования) с целью включения новых факторных показателей.

Моделирование мультипликативных и аддитивных моделей осуществляется за счет разложения одного из факторных показателей на его сомножители:

A = a + b;                 b = c + d;                  A = a + c + d или

A = a * b;                   b = c * d;                   A = a * c * d

Степень детализации и расширения модели зависит от цели исследования, а также от возможностей детализации и формализации показателей в пределах установленных правил.

Кратные модели преобразуются следующими способами:

1. Удлинение.

Для детализации обобщающего факторного показателя на его составляющие, которые представляют интерес для аналитических расчетов, используют прием удлинения факторной системы:

 

 

 

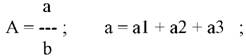
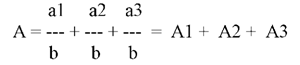
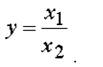
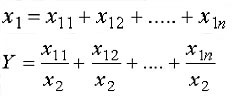
2. Формальное разложение.

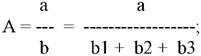
b = b1 + b2 + b3

3. Расширение.

Для выделения некоторого числа новых факторов и построения необходимых для расчетов факторных показателей применяют прием расширения факторных моделей. При этом числитель и знаменатель умножаются на одно и тоже число.

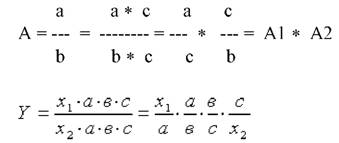
4. Сокращение.

 

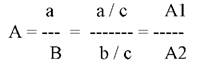
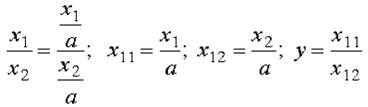
Для построения новых факторных показателей применяют прием сокращения факторных моделей. При использовании данного приема числитель и знаменатель делят на одно и то же число.

Процесс   моделирования   сложный   и   ответственный   момент. От реальности и точности моделей зависят конечные результаты анализа.

Детализация в факторном анализе во многом определяется числом факторов, влияние которых можно количественные оценить, поэтому большое значение в анализе имеют многофакторные мультипликативные модели.

В основе их построения лежат следующие принципы:

• место каждого фактора в модели должно соответствовать его роли в формировании результативного показателя;
• модель должна строиться из двухфакторной полной модели путем последовательного расчленения факторов, как правило качественных, на составляющие;
• при написании формулы многофакторной модели факторы должны располагаться слева направо в порядке их замены.

Построение факторной модели — первый этап детерминированного анализа. Далее определяют способ оценки влияния факторов.

Бальжинов А.В., Михеева Е.В. Анализ и диагностика финансово-хозяйственной деятельности предприятия: Учебн.пособ., - Улан-Удэ, 2003.